ごきげんようばべるぼぶると申します。
この度トレカハック様に寄稿する形で執筆させていただくことになりました。非常に光栄です。主にワンピースカードゲームについて記事を投稿することになると思います。よろしくお願いします。
今回はワンピースカードゲームにおけるリーサルターンの要求値について解説していきます。
初級編から上級編までリーサルにおける全てをまとめましたので全人類に読んでいただきたいと思っています。
※本記事は性質上数字がとんでもなく出てきます。どうにか耐えていただきますようお願いいたします。
1.要求値とは
そもそも要求値ってなにというところからですが、結論から言うと”守るために必要なカウンター値の総計”を指します。
つまりどういうことかというと例を挙げて解説します。
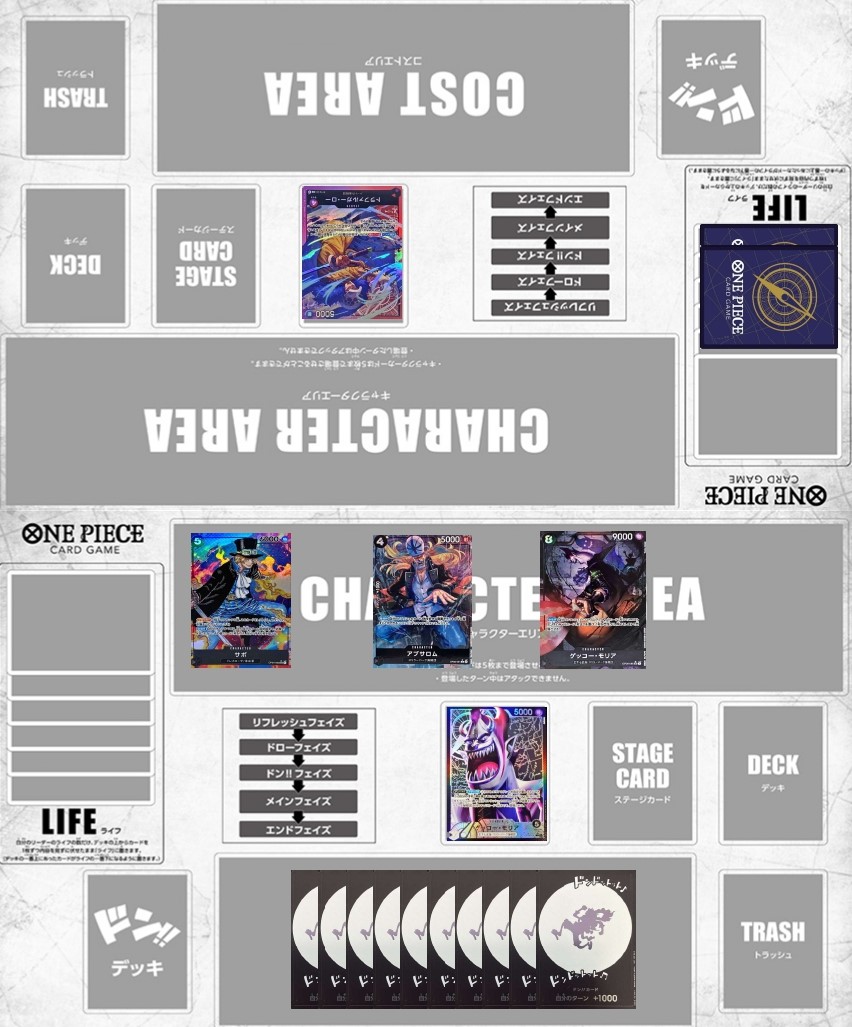
上記は自分側のリーサルターンで相手リーダーの打点は5000,盤面にブロッカーは0体、ライフの枚数が2枚でこちら側は5000のリーダー、5000のキャラ、6000のキャラ、9000のキャラの計4体のアタッカーに加えて10ドンが振れるという状態です。こちらはアタックを3回通せば勝ち、逆にいえば相手はアタックを2回止めることが出来ればこのターンは負けないという状況です。
ここで例えばアブサロムに3ドン、サボに3ドン、リーダーに4ドン振ると盤面の打点は8000,9000,9000,9000となります。これらで相手のリーダーにアタックした場合、相手が負けないためには2回アタックを止める必要があるので8000,9000を止めるか、9000,9000を止めるかのどちらかになりますね。
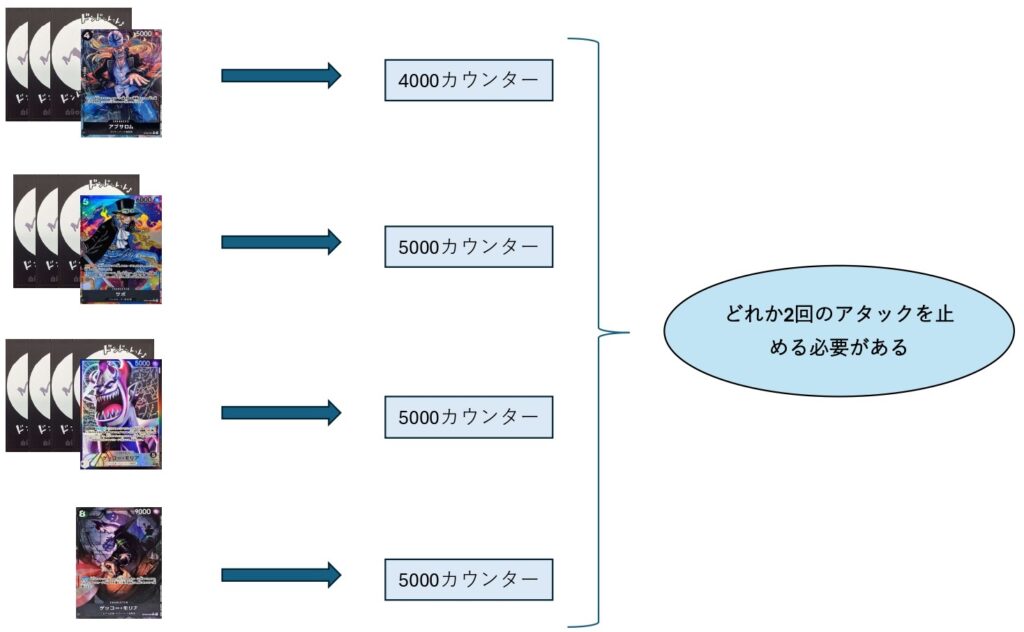
8000を止めるためには4000、9000を止めるためには5000とそれぞれカウンター値が必要になりますのでこれにおける要求値は9000~10000となるわけです。
要求値の概念は以上になります。要求値はアタックの仕方やドンの振り方によって大きく変わっていきます。当然ですが要求値は大きければ大きいほど勝ちやすいです。例外を除いてほとんどの試合で訪れるリーサルターンで毎回最大の要求値を取れるようにしてアタックの仕方のミスで負けないようにしようというのが本記事の目的となります。
2.リーサル時の計算方法について
2.1打点の振り分け方
このゲームは自由に振ることが出来るパワーとして10ドンあります。このドンの振り方によって要求値は大きく変わっていきます。
先ほどの例では8000,9000,9000,9000と振ったことによって9000~10000の要求値となっていました。これを極端に6000,6000,11000,12000と振って考えてみましょう。
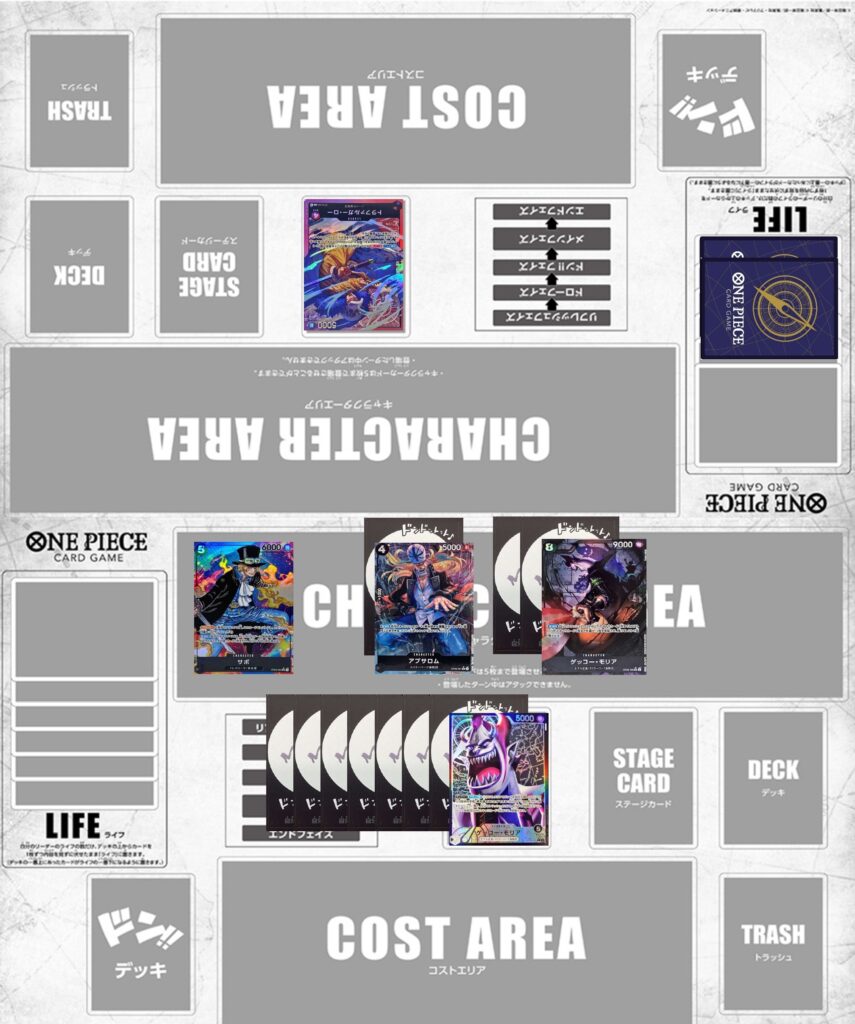
アタックを止めるために必要なカウンター値はそれぞれ2000,2000,7000,8000となりました。
相手はこのうち2回のアタックを止めれば負けないのでパターンとしては4000,9000,10000,15000の要求値となります。
最大値は先述した例よりも高くなりますが最低値は先述の例よりも小さくなってしまいます。
相手としてはこのターン負けなければターンは続くことや自分の手札のカウンターと相談し今後の大きい打点でのアタックを防げそうにないことを考慮し、最初の打点である6000を守るというのが基本的な思考になります。
理想論では15000要求になりますがほぼほぼというか絶対にその要求値になることはありません。必ず低い要求値のほうで守られてしまいます。
こういった形で要求値の振り幅が大きくなってしまうと最低値の要求値で守られた場合のリスクが大きくなってしまうためアタックの打点は出来る限り振り幅が大きくならないようにすることが望ましいです。
今回の極端な振り幅を作ることはありませんが状況によっては多少の振り幅を付けるべき場合があります。どういった場面かは次項で解説していきます。
2.2打点につけるべき振り幅
同じく先述した例を基に解説していきます。
8000,9000,9000,9000の振り分けでアタックした場合要求値9000~10000としていましたがこれは実は2種類の要求値ではなく細かく分けるともっと多くのパターンの要求値になっています。
どういうことかというと8000からアタックしたとき相手が守るためには現状の手札の状態で4000を切る必要があります。
そのままライフへのアタックを受けないまま9000にも5000を切った場合は現状の手札から計9000切ることになりますね。
あるいは8000のアタックを受けて9000のアタックも受けちゃって後の9000,9000を5000,5000切って止める場合もあります。
前者の状況をライフ無9000要求、後者の状況をライフ2込10000要求となります。
相手側として一番得をしそうなのは最初の8000を守って9000,9000を受けて最後の9000に5000切る”ライフ2込90000要求”をアタックの要求値と考えるのが良いです。8000さえ最初に守ってしまえばあとの9000の3回アタックはライフを受けてカウンター。
基本的に相手もアタックされたときに残りのドンを残っているアタッカーを見ながら出来るだけ安く、守り易くしようと考えるため要求値は一番低いラインを考えるのが望ましいです。
では上記のライフ無9000とライフ2込9000の違いですがこれは単純にライフを手札に変換する前後の違いですね。
前者は現状の手札から、後者はライフ2枚を手札に加えてからカウンターを切ることになります。
当然ですがライフからカウンター値を引くことを考えるとライフ込のほうがカウンター値を作りやすいし守り易くなります。
ライフは1枚おおよそ1000カウンターついていることが多いです。
単純にデッキのカウンター値の最頻値は1000であることや期待値も約1000になってることがほとんどだからです。
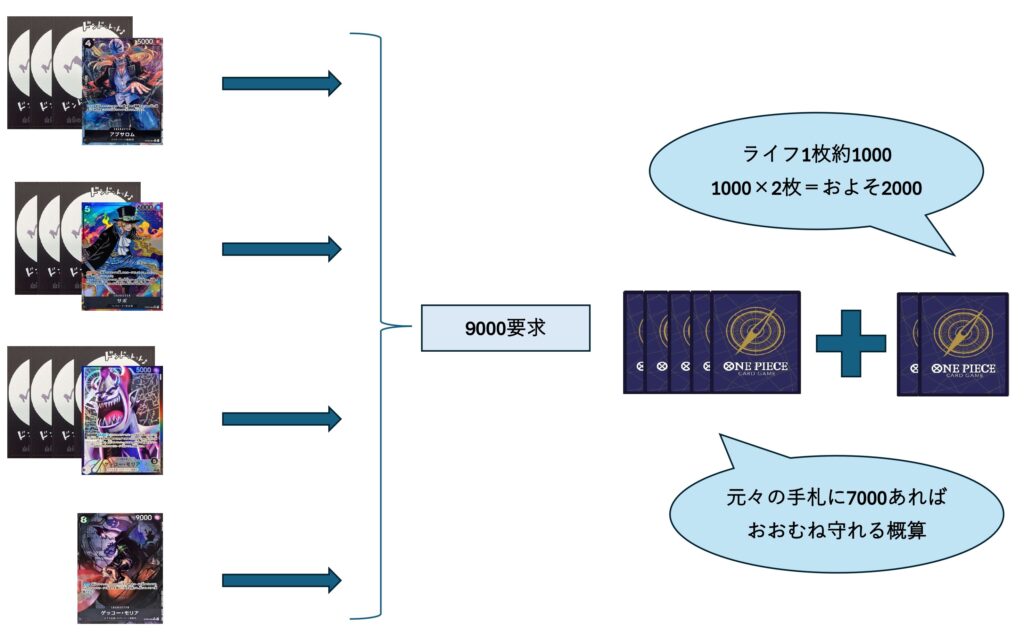
つまりライフ2枚をそれぞれ1000だと仮定した場合に先ほどのライフ2込9000要求は現状の手札に7000あればおおよそは守れるということが分かります。
これだと実質的にはライフ無7000要求にしかなっていないということです。
例えばこれが8000,8000,9000,10000という振り分けだとどうなるか考えてみましょう。
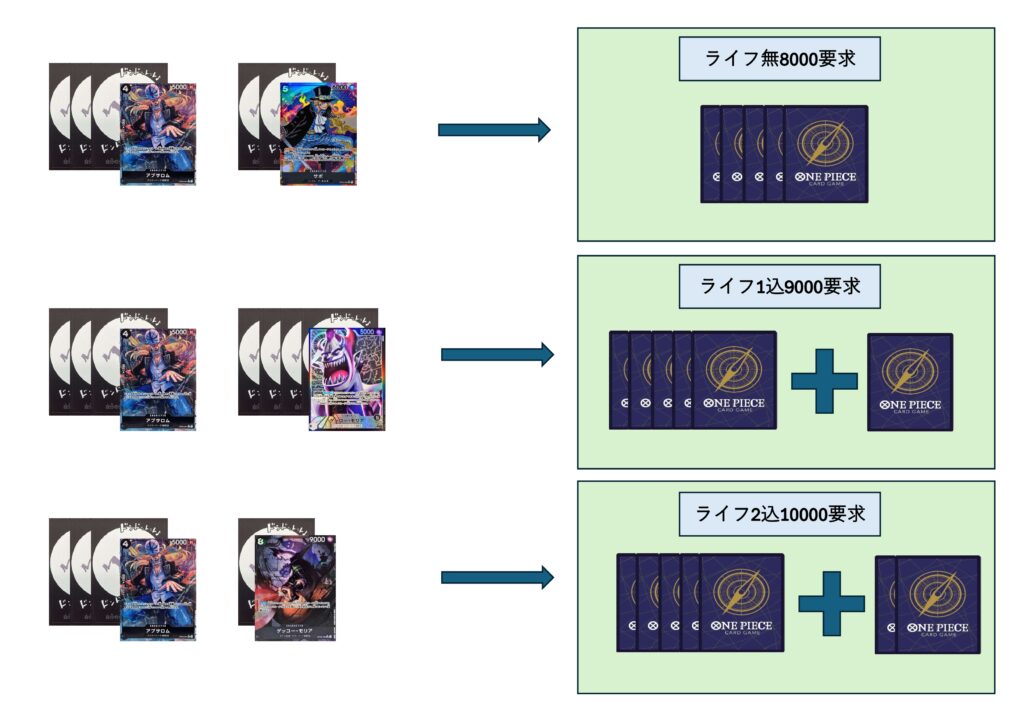
それぞれのアタックを守るためには4000,4000,5000,6000必要で要求値としては8000,9000,10000くらいになると思います。これらをライフを手札に変換する前後も考慮して整理をするとライフ無8000,ライフ1込9000,ライフ2込10000となりました。
8000,8000を両方止める場合は必要なカウンター値は8000と後のアタックを守るときよりも小さいがライフを手札に変換できていないため現状の手札から捻出する必要があります。
8000,9000を止める場合はライフは1枚受けて手札に変換出来ているものの9000必要となっており、ライフ1枚を1000と仮定した場合でも現状の手札で8000は持っていなければいけない計算になります。
8000,10000を守る場合は10000必要でライフ2枚をそれぞれ1000と仮定した場合でも現状の手札で8000要求できています。
ライフ1枚を1000と仮定した場合どのパターンでも現状の手札に対して8000の要求が出来ているとわかりました。
最初に挙げた8000,9000,9000,9000の例ではライフ2込9000要求、つまり現状の手札に要求できていたのは7000であったた
め、この振り分けよりも8000,8000,9000,10000の振り分けのほうが要求値が高いことが分かりました。
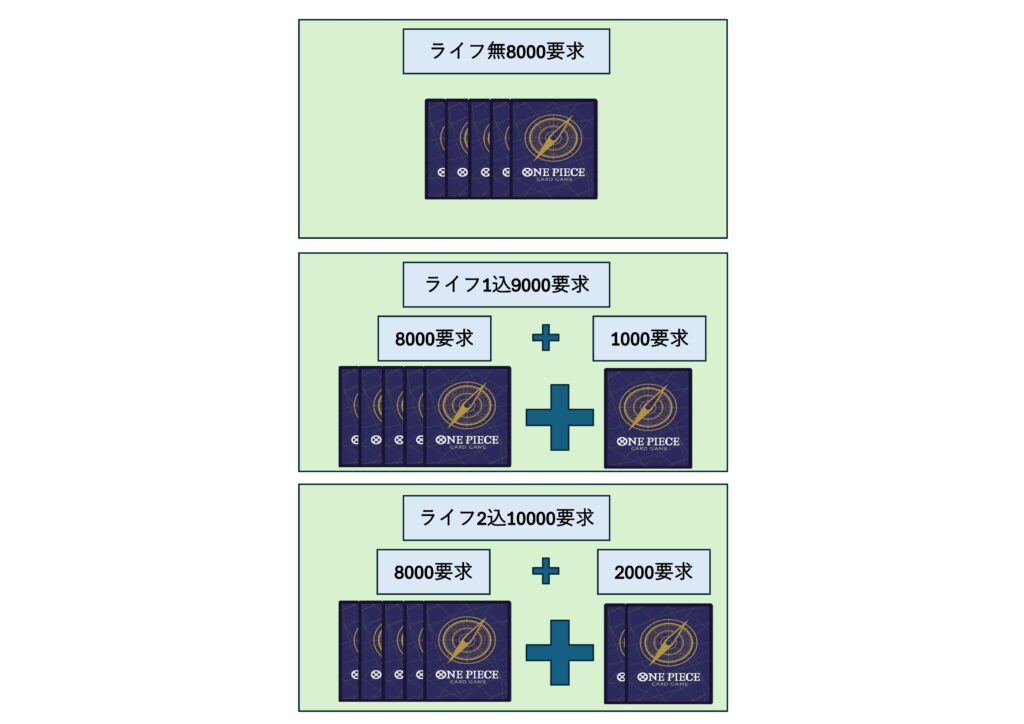
このようにライフを1000換算した場合にそれと相殺する形で要求値を段々にあげていくことが必要でこれが打点を振り分けるときに付けるべき振り幅になります。
この打点を段差がある状況を僕は階段をつくると便宜上呼んでいます。
階段という単語は最近ではそれなりに普及してきて割と他の媒体でも目にすることがあるようになったので覚えておくといいかもしれません。僕も今後多用していくと思います。
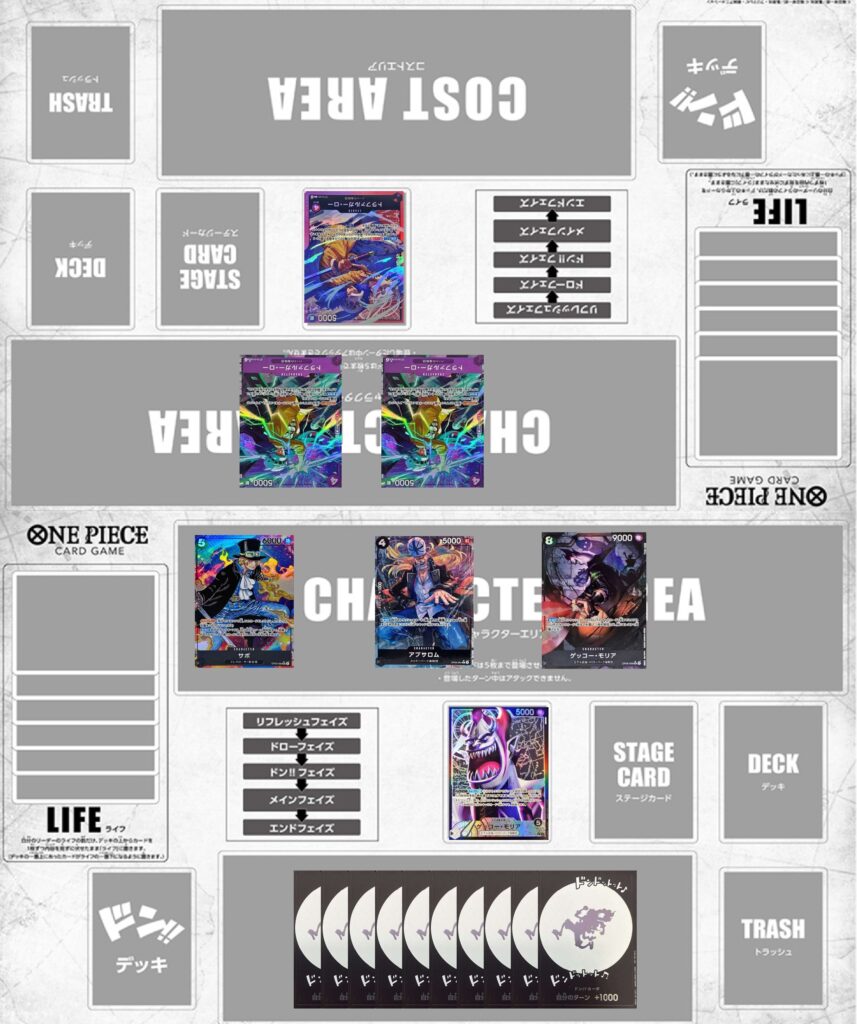
これがもし相手のライフが0でブロッカーが2体いた状況を考えてみましょう。
この時の8000,9000,9000,9000と8000,8000,9000,10000を考えてみます。
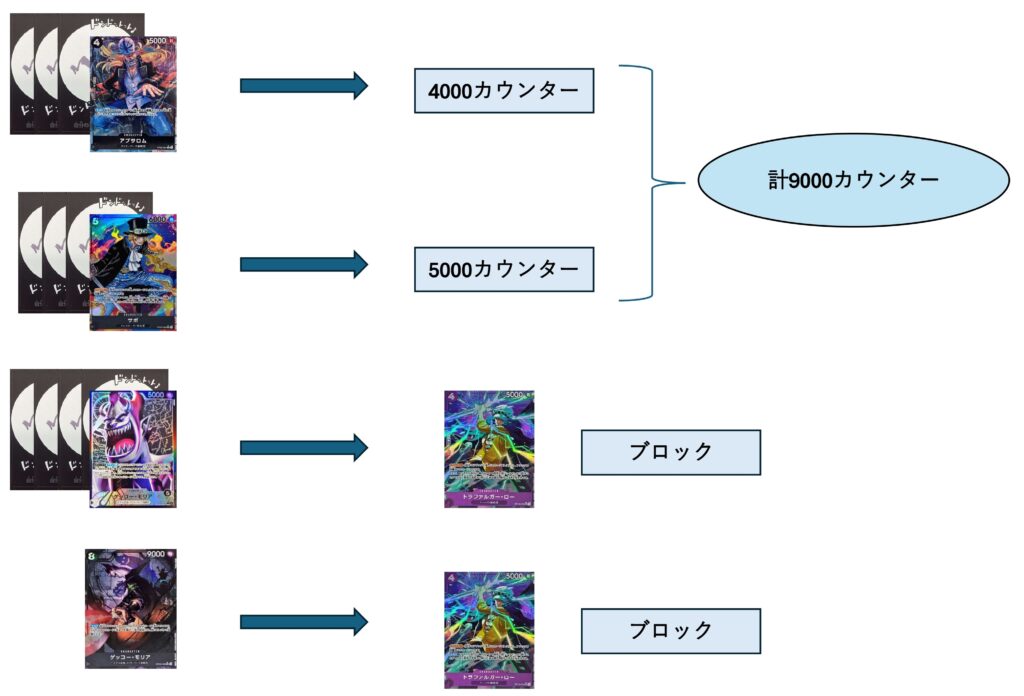
まず前者はこうなりました。
相手は要求値が高い箇所をブロッカーを使用し、低い方を手で守るのが安い受け方になるため8000,9000にカウンターを切り9000,9000はブロックをすると考えると要求値は9000となりました。
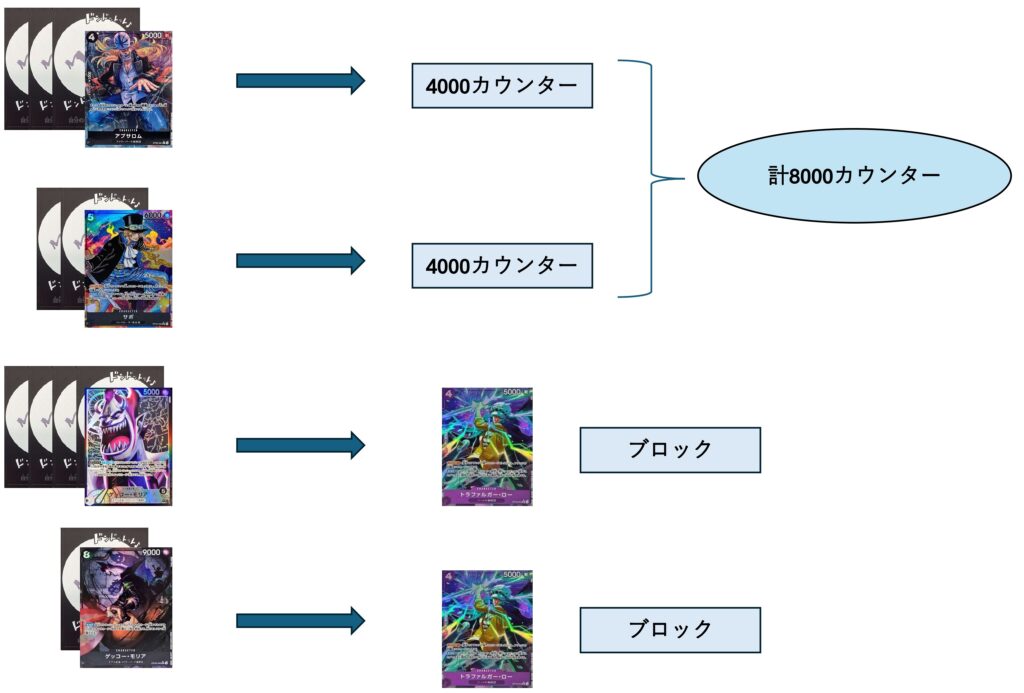
続いて後者ですが同様に安く受けるように考えると8000,8000を手で守って9000,10000に対してブロッカーを使うとしたときに要求値は8000と前者よりも下がってしまいました。
打点に階段を作るのはライフ1枚を1000カウンターと仮定するからであるためライフがないこのような状況においては打点に振り幅はつけないほうが良いと分かります。
ライフがある時は階段、ブロッカーがいるときは均等と覚えておくと分かりやすいです。
ここまでがアタックにおける基本になります。まずは以上のことを身に沁み込ませて脱初心者です。
2.3複雑な状況での思考
ライフがあるときは階段、ブロッカーだけのときは均等は分かったけどライフ1ブロッカー1のような状況はどうするんだとなったりするでしょう。未だに僕も悩みます。
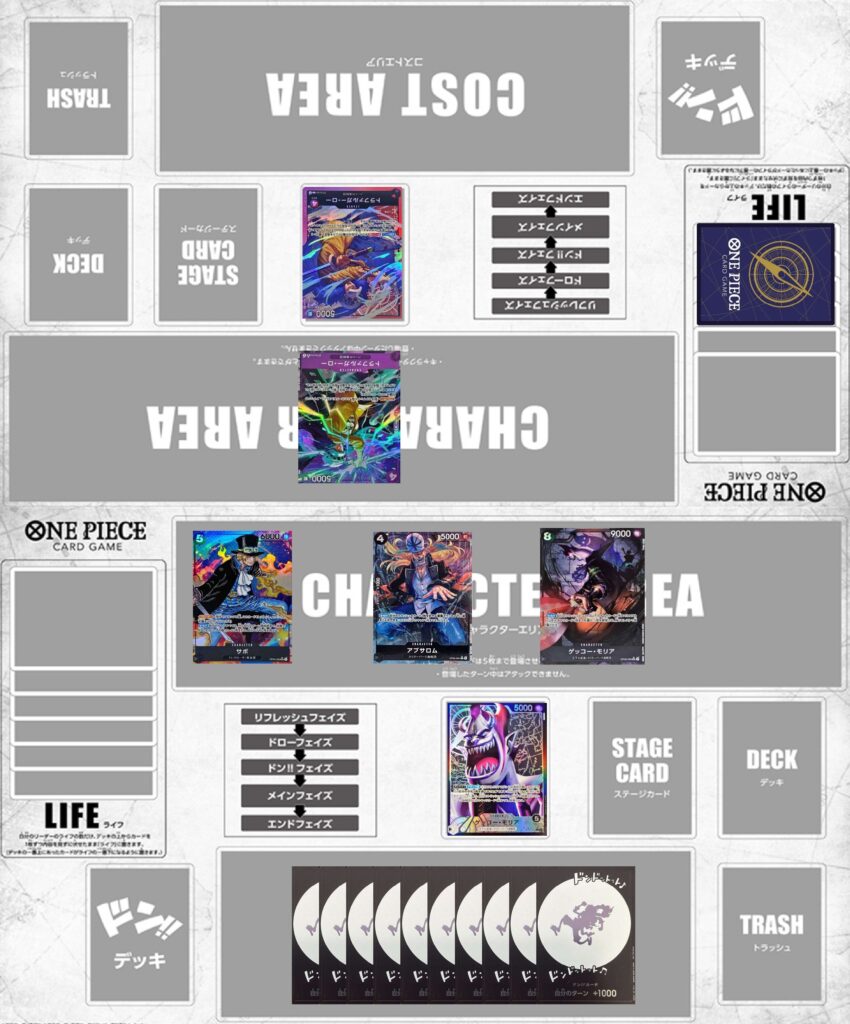
ではこちらの盤面は前項同様の状況で解説していきます。
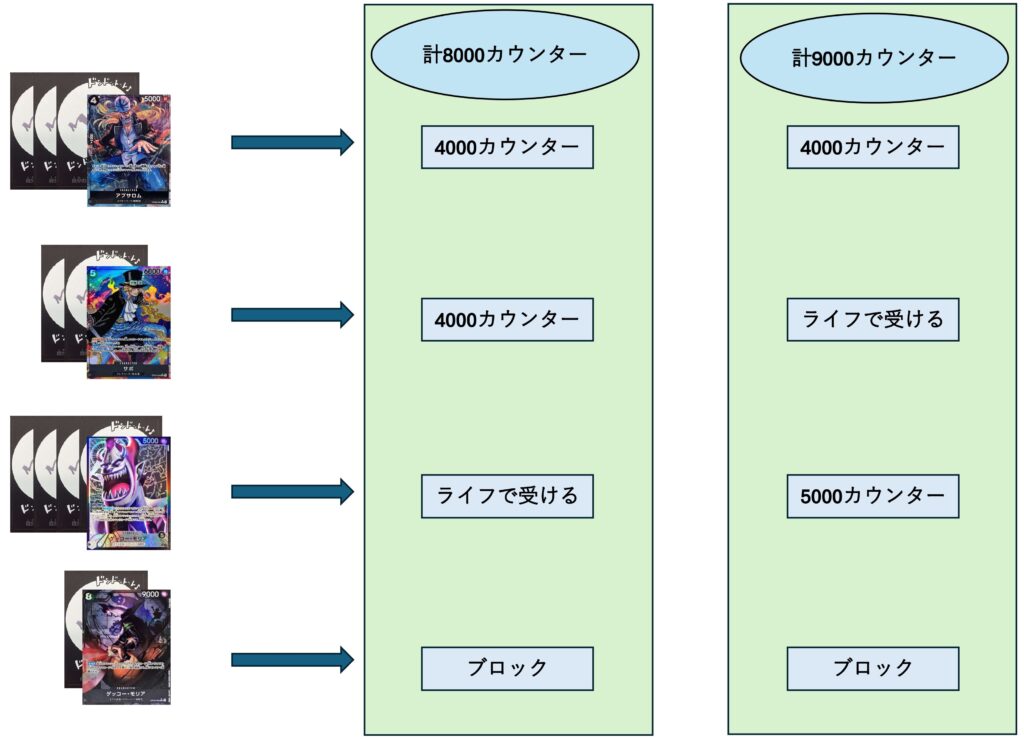
これは8000,8000,9000,10000でアタックした場合です。
ライフを貰う前に8000,8000を手で守って9000,10000をライフとブロッカーで受ける、8000を手で守ってライフ受けてから8000,9000を手で守って10000をブロックするのおおよそ2パターンになります。
ライフ無8000~ライフ込9000要求となります。
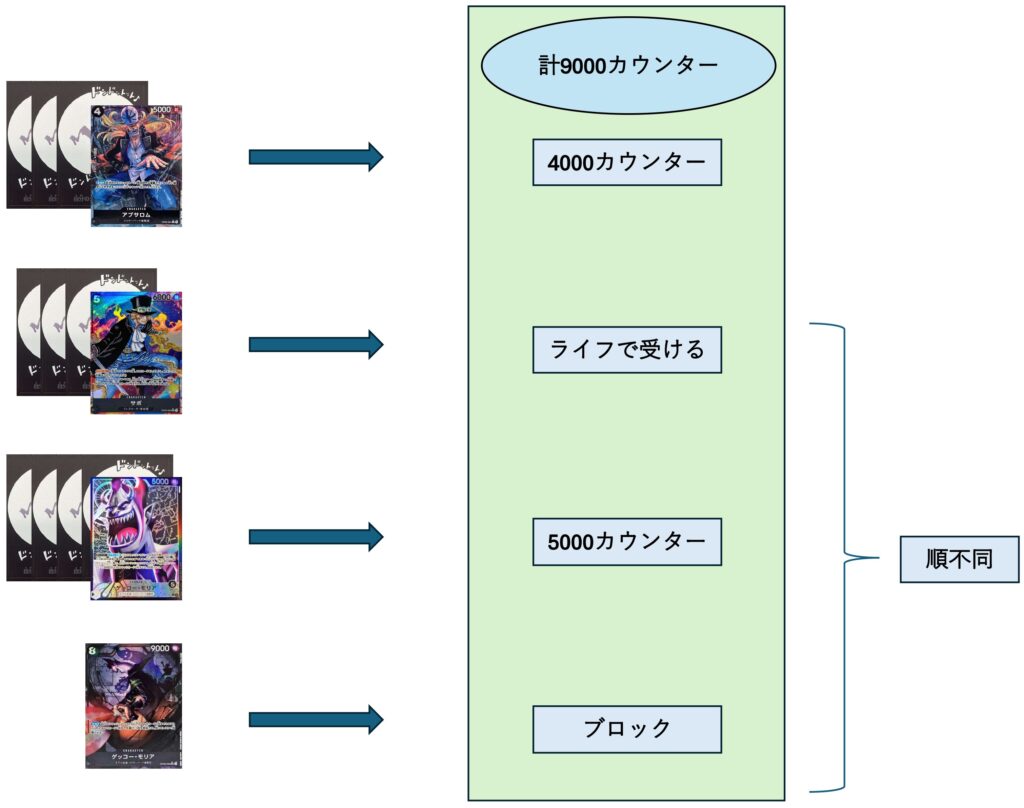
続いて8000,9000,9000,9000でアタックした場合です。8000を手で守って9000を貰ったあと9000,9000をブロックと手で守るの1パターンのみになると思います。ライフ込9000要求です。
両者とも同じように見えますが実は後者のほうが僅かながら要求値が高いです。
これは現状に手札に8000カウンターあった場合を考えると前者は8000,8000に対してライフを受ける前に4000,4000とカウンターを切ることが可能なのでライフ無8000要求で守られてしまいますが後者は8000は守れても9000に対して残り4000しか持っていないため受けざるを得ず、ライフ込の要求までは確実に行えます。
ライフが1000であれば結局アタックは通りませんがライフのカウンター値が0だった場合は貫通してリーサルとなります。
前者は手に8000持つ&ライフのカウンター0でも守り切られてしまいますが後者に対しては手に8000持つ&ライフのカウンター0であった場合貫通して勝つことができます。
後者はライフのカウンター値0~2000の抽選を行うことが出来るため僅かに要求値が高く出ました。
判断としてはブロッカーが残っている以上は均等でいくしかないと考えるのが良いと思います。
しかし、ライフがもっと多くなった場合は階段を作るべきとなるので複雑な状況であればその時に応じて考えてみる必要がありそうです。
自分で考えるためにも理論と計算の仕方を根本から理解する必要がありそうですね。
2.4打点の振り分け先
念のため、そもそもなぜ打点を振り分ける必要があるのか、どんなキャラにでも振り分けるべきなのかを解説しようと思います。
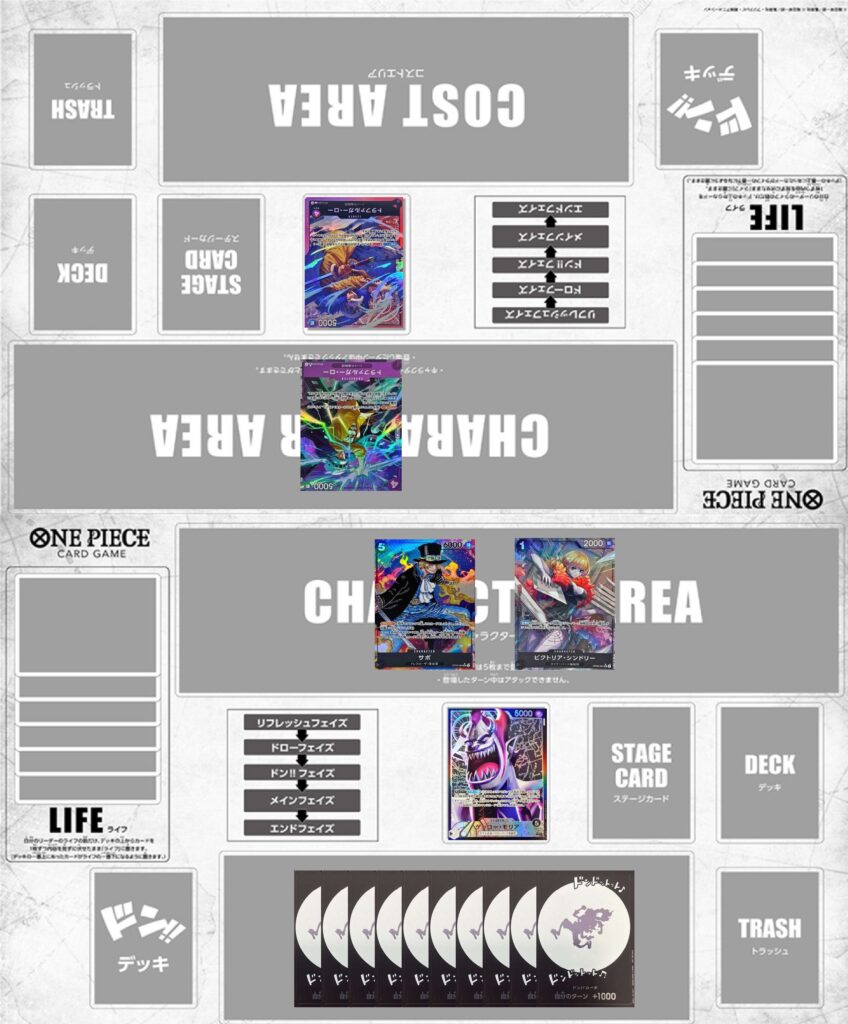
相手のライフは0で、ブロッカーは1体に対してこちらは5000,6000,2000の打点を持つ盤面となっています。ブロッカーがいるため攻撃回数は最低でも2回は必要でしょう。
シンプルに振り分けるなら10000,11000となり、10000に対する6000が要求値となります。
こういう状況で2000のキャラもアタックに参加させた場合はどうなるでしょうか。
3体でアタックするのだとしたら打点は7000,8000,8000となり、8000はブロッカーで止まるものの、7000,8000に対する3000+4000の合計7000が要求値となり先ほどよりも高い要求値となりました。
2回アタックの場合合計打点を2で割った打点の1回分が要求値になるのに対して、3回アタックでは合計打点を3で割った打点の2回分が要求値になるためです。
相手が手札で止めなければいけない攻撃回数は多くなればその分要求値も上がりやすいため、普段アタッカーにならないような打点のキャラにもドンを振る意識はしたいものです。
3.理論的に考える
ここまでは定型的な場面での解説になりましたが本項では様々な場面に対応するためにおおもとの考え方についてを解説していきます。
先ほど2.3項で挙げた例を使ってみます。
この場合の振り分けは8000,9000,9000,9000であるのがいいという結論になりましたがこれを実戦で検証できるようになる必要があります。
要求値は基本的に相手が一番守り易い形で考えるのがベストなのでブロッカー及びライフは無限カウンターとして有効に発揮させた場合で考えていきます。
そのためそれら無限カウンターはこちらの打点が大きい順に相殺していくと考えるのが手っ取り早く簡単だと思います。
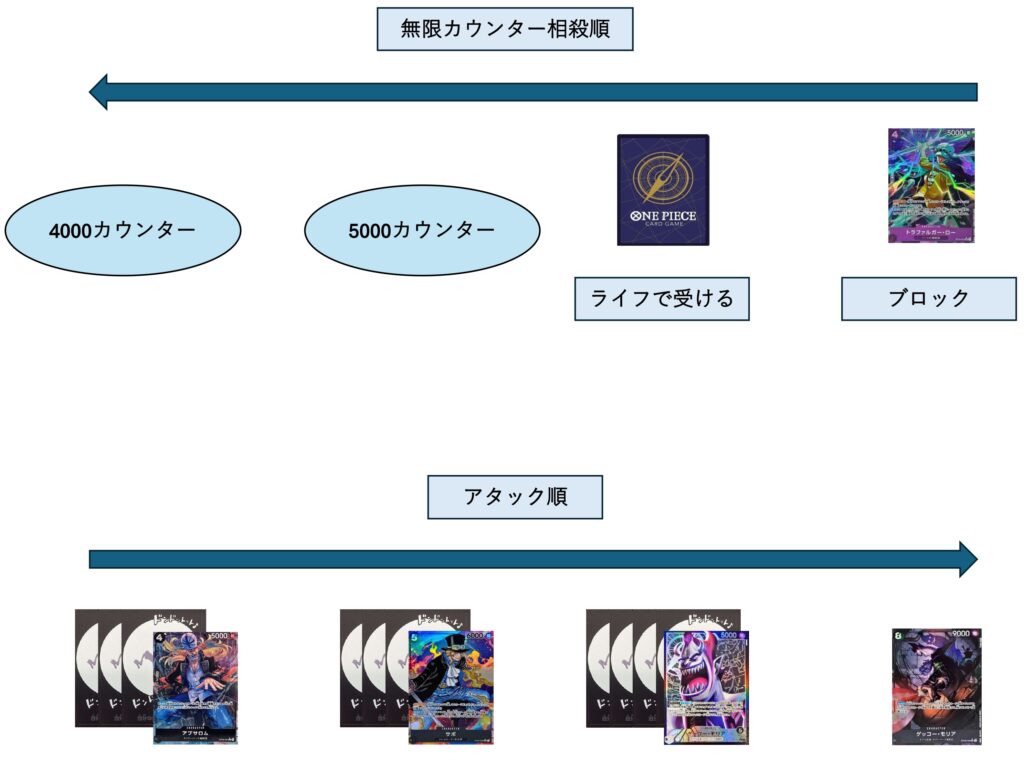
こうなりました。先述していますが要求値はライフ込9000要求ですね。
検証ということで別の択であった8000,8000,9000,10000の場合も考えてみましょう。
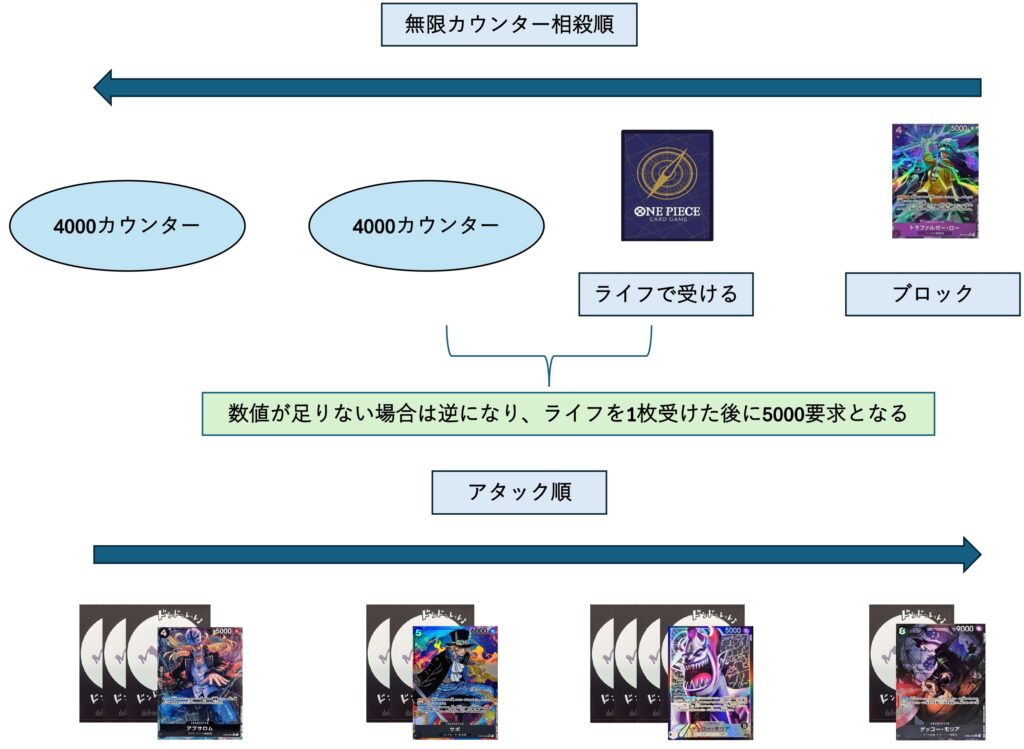
こうなります。こちらも先述通りライフ無8000~ライフ込9000要求です。
こうすることによってそれぞれ相手が手札からいくつ必要でライフやブロッカーはどのタイミングで使用していくのかが分かりやすく、どちらの振り分けが要求値が高いのかの精査がしやすくなります。
上記の例ではあんまり役に立つ実感がわかないと思うので新たに別のシーンを見てみましょう。
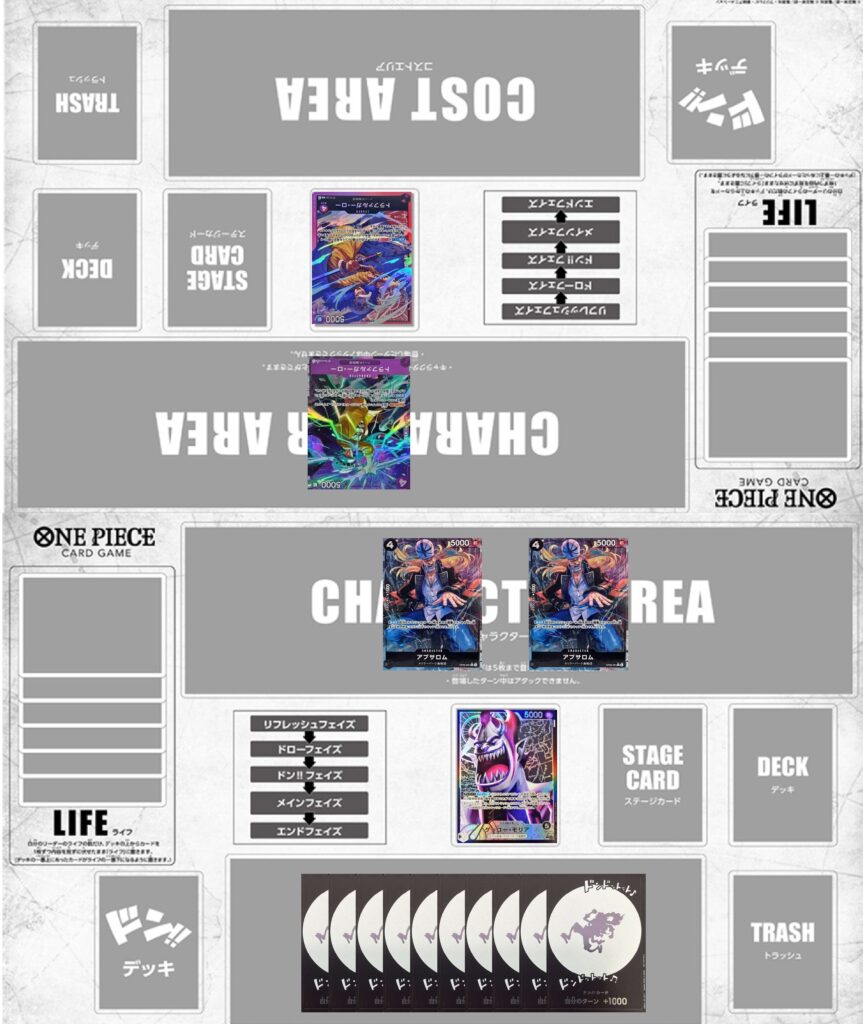
5000のアタッカーが2体と5000のリーダーが1体という状況に相手のブロッカーが1体、ライフは0枚という状況です。ブロッカーのみという状況なのでここまでで学んだように振り幅が大きいと、大きい打点がブロッカーという無限カウンターと相殺してしまい要求値が下がってしまうのでここは均等に打点を振り分けましょう。
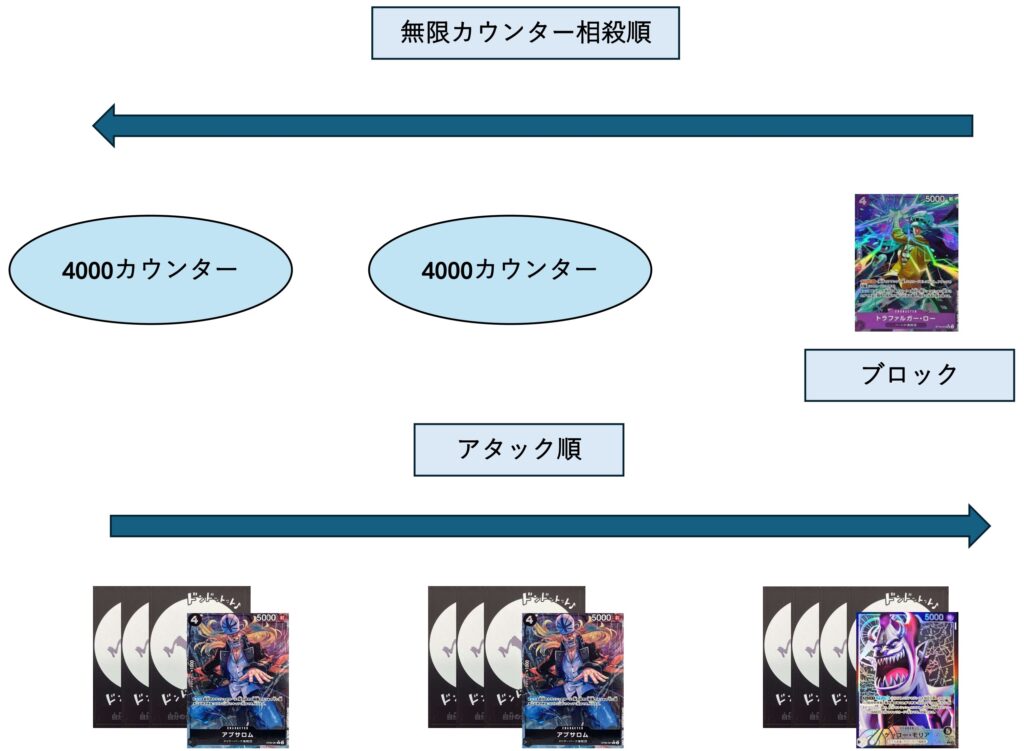
8000,8000,9000となりました。この項でも記載した通り一番大きい9000という打点がブロッカーと相殺するので要求値は8000,8000に対する4000×2の合計8000とまとめることが出来ました。
基本的にアタックは小さい順ですがそれはライフが相手の手札に加わることで増えるカウンター値に対して合わせるためであるためこういうシーンにおいてはアタックの順番はあまり気にする必要はありません。
9000からアタックした場合当然3分割のなかで一番大きい打点であるため相手はブロックしてくるのが基本でしょう。その場合は残りの8000,8000は5000,11000や6000,10000と振り分けても要求値は変わりません。面白いことにブロックされる打点よりも大きい打点を作れたりします。
上記の考えは、9000がブロッカーと相殺されたのちに5000×2回+6ドン分が要求値になると整理することができます。
実はこれに大事な要求値の話が隠されていますがそれは4項で解説するとして、こういったように相手のブロッカーやライフで相殺することで要求値をキャラの素体+余っているドンと独立して考えることができ、これを覚えておくとかなり複雑な状況にも対応できるようになるため覚えておくと実践時に活かすことが出来ると思います。
3.1アタックの順番
これまでアタックは基本的に小さい順にと教育されてきたと思います。が、前項の例においては高い打点、つまり9000からアタックしたほうが良いシーンとなります。
ここでは基本的に8000,8000,9000がシンプルな打点なので9000がブロックされる前提で解説しました。9000がブロックされる前提で相手にライフがないのであれば9000からスタートしても要求値に変動はありません。ここで相手はブロックもしくは手札からカウンターを切るわけですが、ブロックされれば予定通りであるもののカウンターを切ってもらえた場合は8000,8000のアタックの片方をブロック、もう片方をカウンターを切ることになりその合計要求値は9000となり上がるわけです。
もちろん計算がちゃんとされていればブロックされるわけですが相手のミスとなる選択肢は与えるに越したことはありません。最後に大きいアタックをするときは相手側に選択肢がないためミスを誘発するきっかけは生まれません。こういった細かいミスの押しつけもカードゲームの醍醐味の一つですね。
4.枚数要求について
3項の例でまとめた通りこれは8000,8000,9000の振り分けで要求値としては8000となりました。が、大きい打点と先に相殺させることで5000×2+6ドンが要求値になるため実は8000,8000という打点で振り分けるよりももっといい振り分けが存在します。
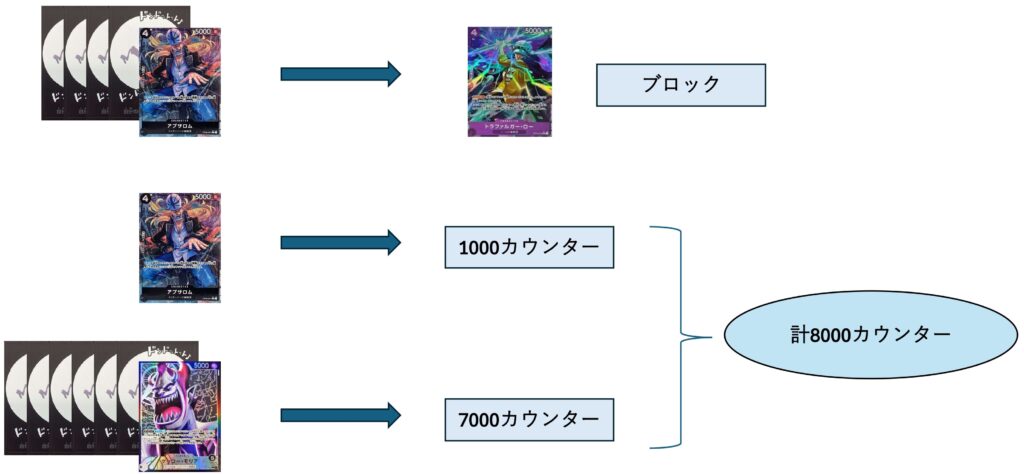
9000,5000,11000の5000,11000に対する8000要求です。同じ数値の要求値ではありますが相手が切る必要がある手札の枚数はこのパターンのほうが1枚多いです。実際に数えてみます。
8000,8000という振り分けには2000カウンター2枚×2回で最低4枚要求となりました。
対して5000,11000という振り分けは5000に対して1000×1枚、11000に対して1000×1枚,2000×3枚の合計4枚7000カウンターで枚数としては最低5枚要求となりました。
これらの差は8000,8000は2000×4枚持ちを貫通することはできませんが、5000,11000は2000×4枚持ちを貫通することが可能で明確に差があります。単純に枚数要求は多い方が優位です。
ちなみに5000,11000でなくとも7000,9000も2000×4枚持ちを貫通することが可能ですが若干前者のほうが優位です。0コスカウンターイベント×2+2000カウンター持ちに対して後者は貫通できませんが前者は貫通可能です。本当に若干の差ですが笑
ワンピでは漠然と7000,9000のような打点を作りがちですがこれには枚数要求という側面があるわけですね。
当然ニューゲートのような6000打点のリーダーに対しては8000,10000のような形で2000刻みの差を付けることで枚数要求が1枚ずつ上がります。
相手リーダー打点+2000xを理解しておけば良いと思います。
リーサルにおいては数値としては同値であれど枚数の要求も併せて考えるということも頭に入れておきたいですね。
4.1忘れがちな枚数要求
相手の場にブロッカーもライフもない、残りドンをアタッカーに全部付けてアタックするといういわゆる全ドンパンチをするシーンは結構あると思います。が、その際に自分の場に4000のキャラはいませんか?
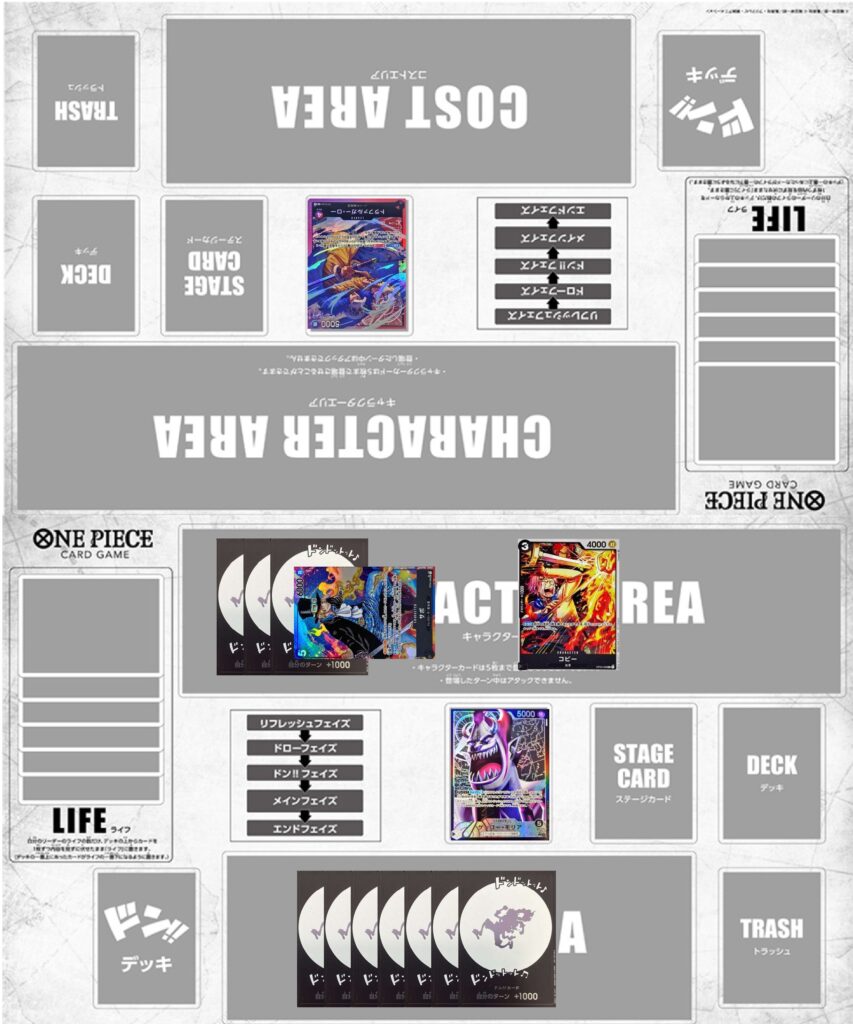
例えば既に5000以上のパワーを持つキャラはアタック済みで残りは4000のキャラと自分のリーダーのみ、ドンは7ドン残ってて相手の守りはもう手札だけという状況。残った7ドンをリーダーに付与して12000アタックしがちですが実はこの状況1ドンだけは4000のキャラに振ったほうが若干お得です。
前項で解説したように同様の数値で要求できるのであれば枚数要求が高い方がよいです。そして今回の例はそれに当てはまります。
リーダーに7ドン振った全ドンパンチは12000アタックとなるため要求値は8000です。8000が作れればどんな組み合わせでもよいですね。枚数は最低4枚要求です。
対して4000に1ドン振り、残り6ドンをリーダーに振ったアタックは5000,11000となり、それぞれ1000,7000必要で合計8000要求です。前者と数値は同様ですが、枚数はそれぞれ最低1枚、4枚の計5枚要求となります。
注意ですが、このような全ドンパンチの状況は場の3000のキャラに振ってもそれは要求値が下がってしまうだけなのでそれだけはしないでください。あくまでも1ドン振ればアタックが可能なキャラのみで行える行為です。
また、かなり珍しいレアケースですが同様な状況で残りドンは8ドンある場合、リーダーの全ドンパンチは13000で要求値は9000、枚数は最低5枚です。
1ドンをキャラに振って5000,12000でアタックした場合も同じく要求値は9000の5枚要求です。
一見同じように見えますがめちゃくちゃ薄い線で後者のほうが貫通可能なパターンが存在します。これは前項例と類似したもので、0コスカウンターイベント+2000カウンター×3の場合です。
本来9000要求でちょうど守れていたアタックであったものの、振り分けた場合には1000要求に2000を切らざるを得ずにその後の12000アタックに対して1000足りなくなってしまいました。
上記のようなパターンはほとんどありませんし、考える必要もないです。全ドンパンチの際に場に4000のキャラがいれば先に1ドン振ってアタックしてから全ドンパンチするという習慣さえつけておけば裏目はないはずです。
相手のライフが取れてブロッカーもいなくてあとは全ドンパンチで祈るだけだ!というシーンも一度落ち着いて冷静に最後まで気を抜かずやり遂げましょう。
4.2相手の手札枚数を考慮する
続いては相手の手札枚数から打点を流動的に作るポイントについて解説していきます。
例えば以下のような状況。

場には5000,5000,6000,6000のキャラ4体とリーダー、相手のライフは2枚で手札は4枚というシーンです。
ライフが2枚あるので1000,1000と仮定し、ライフ無の要求値とライフ2込の要求値に2000程度の差を付けるのが望ましいです。相手がいつ受けていつ守るのかというのは不明なのでとりあえず頭の中で均等に振り分けてみます。
7000,7000,7000,8000,8000となりました。とりあえずこれをベースに打点の振り分けを考えてみます。
現状ではライフ無9000要求~ライフ2込10000要求となっています。が、これは数字上の話で実際の状況ではありえないパターンがあります。そうです、相手の手札が4枚の状況でライフを2枚とも残しながら9000カウンターを切ることは不可能であるためライフは最低でも1枚は7000打点で削ることがこの時点で分かります。また、ライフ1枚受けて手札が5枚になったとしても7000を3回止めることはできないのでアタック前には7000でライフが2枚とも取れることが分かりました。
また、7000が2回ライフに通り、残りの7000の2回アタックに対して手札を2枚ずつ計4枚使用するとなると相手の手札は残り2枚で最後の9000アタックに対して最低でも3枚必要なのでそもそもこの状況は確定リーサルであることがアタック前には分かりました。
このように相手の手札が少なく、こちらが要求する枚数が相手の手札の総数を超えている場合はいわゆる確定リーサルとなります。そのうえでこういった枚数の差がシビアな状況においては均等な振り分けや1000ずつの階段を作成することよりもリーダー+2000xという枚数要求をしたほうが良いことがあるため状況に応じて数値で要求するのか、枚数で要求するのかといった判断と柔軟な対応が必要です。
確定ではない場合は特に柔軟に考える必要があります。例を見てみましょう。

場には5000,5000,5000,5000,6000と5面展開でリーダーは5000、対する相手はブロッカーはいないもののライフが3枚と手札が2枚です。もうすでにアタック回数や相手のライフが多く複雑ですね。
平均的に振り分けた場合は6000,7000,7000,7000,7000,7000の6回アタックとなりました。受け方としては一番低い6000を守るのはマストですがそれ以降は全部受けた後に7000アタックを2回止めることになると考えるとライフ3込8000要求です。
相手の手札の数値の持ち方とライフというランダムなカウンター値にどれくらい要求できているかというと相手の手札に2000が2枚あったとしたらライフ3枚で合計4000必要になりますし、手札に2000,1000と持っている場合はライフから引くカウンター値は計5000必要になるというような状況です。
これを相手の手札の枚数に合わせた振り分けをしてみると要求値が格段に上がります。
5000,5000,5000,7000,9000,10000という振り分けで順にアタックしてみるとどうでしょうか。
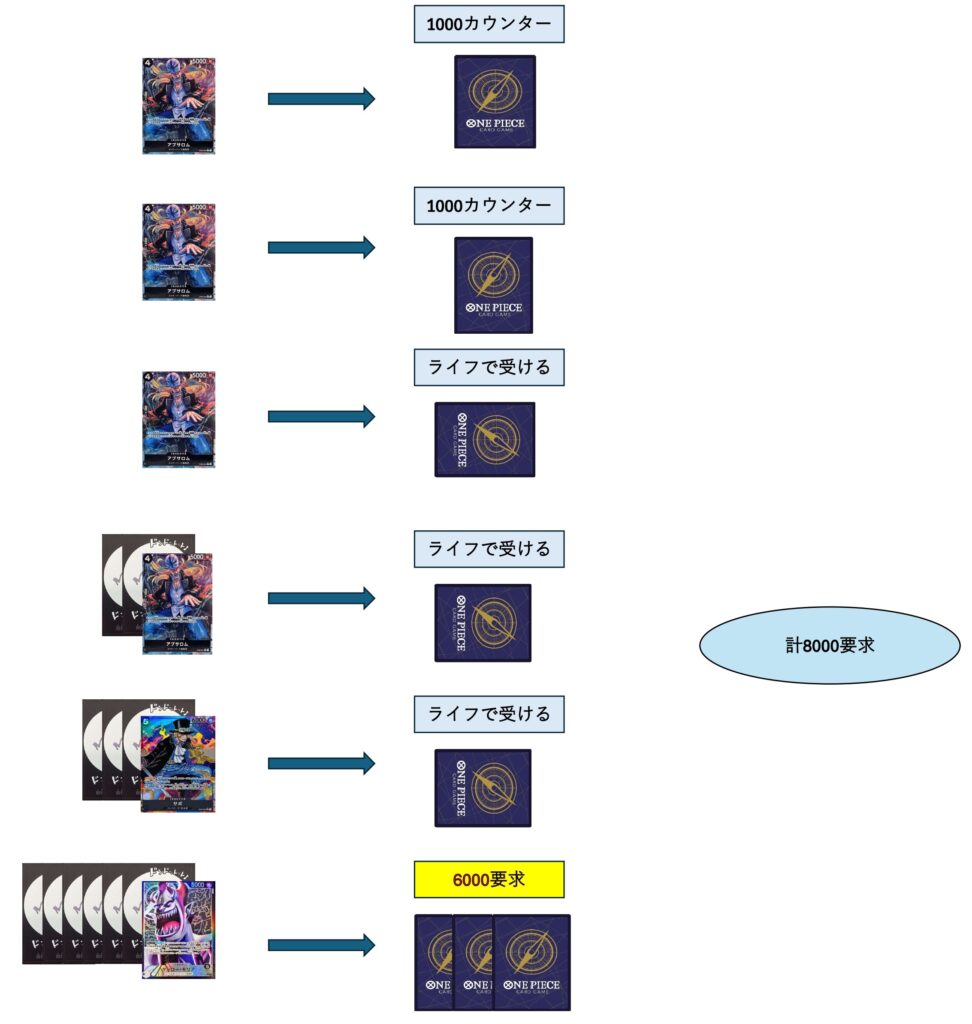
最初の5000での2回アタックは安いので止めたいところですが止めてしまうと3回目の5000が確定で通ってしまい、7000,9000とそのまま全て通ってしまいます。そうするとライフから持ってきたカウンター値で最後の10000を止めなくてはなりませんが6000必要となるために要求値は先ほどの例と同様にライフ3込8000要求となりました。
数値としては同じに見えますが相手の持ち方が2000を元々2枚持っていたとしても5000に切らざるを得ないためにライフから合計6000必要であるということは変わらないため要求値としては前者よりも格段に上がっています。
これまでに解説してきた極端な振り分けは要求値を落としてしまう、だとか相手は安く守るために低いアタックにカウンターを切るといったことに相反して要求値を上げることができました。
ちなみに最初の5000を守って2回目の5000を受けるというような場合は次のアタック以降を7000,7000,7000,10000となり、確定リーサルとなってしまうため最初の5000アタックは2回とも守らざるを得ません。
相手の手札が少ない状況はこのように相手がアタックを守るべき回数とカウンターとして切らなければいけない枚数を考慮し、可能であれば小さい打点で相手のライフを取ることで振り分けに幅が作れて相手のライフに対する要求値を上げることができます。
また、相手の手札に合わせて打点を変えていくことで要求値を上げることができるため最初に決めた振り分けで決め打ちするのではなく、相手の受け方で打点を流動的に作ることを意識してみましょう。
5.要求の精査
ここからちょっと難しい話をしていこうかと思います。
4.2項の例においては5000,5000,5000から入るパターンを提示しましたが実際には他にもかなり強い振り分けがあります。
6000,6000,7000,7000,7000,8000です。最初に例に挙げた振り分けにライフ枚数を考慮し、少し振り幅を付けた形です。
最初の6000を止めない場合その後の7000×5回アタックで確定リーサルになってしまうため最初の6000は止まる前提として2回目の6000を止めた場合相手の手札が0枚になるため前項同様に5000のアタックでライフが取れるようになります。
その後は7000,8000,9000と階段になっており最終的にはライフから合計5000要求できることになります。
これがもし2回目の6000を受けた場合7000,7000,7000の内2回は受ける1回は止める形になり、最後の8000を残り手札2枚で守ることになります。
結果としては2回目の6000を止める止めないに関わらず合計9000要求で最初の手札が2000,1000だった場合はライフから合計6000要求で2000,2000と持っていた場合はライフから5000要求となります。
また、4項例の振り分けと比較した場合に明確に良い点があり、1000,1000の持ち方に対しては確定リーサルとなることです。
4項例は2000,2000と持たれていてもライフから合計6000要求できるという良い点があり、こうなるとどっちのほうがいいのかという判断はかなり難しくなってしまいます。
明確に判断するためには確率を用いるしかありません。
というわけで実際に計算してみましょう。手札2枚とライフを確率から計算します。
条件としてはデッキ50枚に対して1000カウンター26枚、2000カウンター12枚、0カウンター12枚とある程度標準的な構築とします。
今回の場合は相手が2000,1000と持っていた場合両者ともライフから6000要求であることは同じです。
そのため相違点である4項例における①1000,1000及び②2000,2000持たれている時のライフ合計6000によって敗着する確率と本項例における③2000,2000もたれている時のライフ合計5000によって敗着する確率を比較します。
計算過程はある程度省略しますが例えば①は26/50×25/49×12/48×11/47×10/46で計算できます。
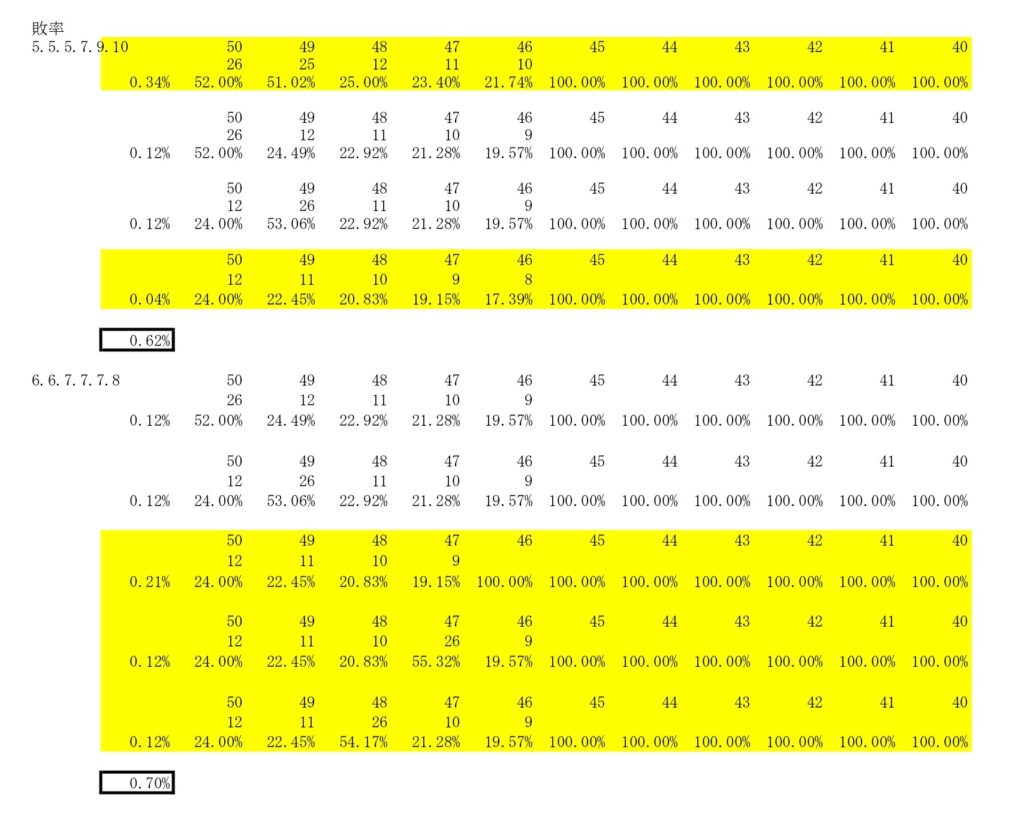
結果としては①0.34%、②0.04%、③0.45%となり①+②<③となりました。
今回は敗着確率を算出したので結果としては前項例のほうが負ける確率は0.07%低いのでおおよそ6項例が優位であると分かりました。
ただ、実戦中にこんな計算は不可能に近いうえに、手札に残るカウンター値は思考が影響するため確率で計算された数値を上回っていることの方が多いです。
そのうえ、差は確率上10000戦に対して7回程度しか勝敗差が生まれないためあまり気にするほどでもないかもしれません。
が、このシーンはあくまでも例で実戦のなかでは10%くらい勝敗に差があることもあるので精査する癖は付けると良いと思います。
この例では手札も完全ランダムで考慮しましたがこれが相手の手札に1000カウンターが見えているとするなら本項例のほうがよく、2000カウンターが見えているなら前項例のほうが良いです。また、相手のトラッシュや場のカードを考慮することでさらに解像度高く判断できます。
この判断をするために先ほど説明したように振り分けごとにこの振り分けでないと勝たないパターンというのを両者挙げて感覚でもいいのでどちらのほうが起きにくそうかということを考えれるようにしていきたいです。
5.1要求値の精査ver話題のシーン
一時話題になりました、相手のライフ1枚に対してa7000,9000かb8000,8000かという問題。これも同様の考え方で判断することが可能です。
aの負けパターンは①3000持たれている場合でbの負けパターンは②3000持ちのライフ1000以上もしくは③2000持ちのライフ2000以上もしくは④1000持ちのライフ3000というパターンです。条件は1000カウンター18枚、2000カウンター9枚、3000カウンター3枚、0カウンター20枚で考えていきます。
とはいえ①については相手の手札の枚数等の状況が分からないため今回は②③④を中心に考えて行こうと思います。
また、相手の手札の分布が分からないので仮に1000持ち:2000持ち:3000持ちの可能性を33:34:33の比重で考えます。
aは1000持ちに対し確定で勝つため勝:敗は33:0です。2000持ちに対し負けるパターンはライフが3000カウンターである場合のみなので3/50の6%が敗率で勝:敗は31.96:2.04となります。3000持ちに対しては問答無用で負けなので勝:敗は0:33で合計としては勝:敗は64.96:35.04となりました。
続いてbを整理します。1000持ちに対し負けるパターンはライフが3000カウンターである場合のみなので3/50の6%が敗率で勝:敗は31.02:1.98となります。2000持ちに対して負けるパターンはライフ2000カウンター以上の場合なので12/50の24%が敗率で勝:敗は25.84:8.16、3000持ちに対してはライフが数値持ちなら負けなので30/50の60%が敗率で勝:敗は13.2:19.8となりました。合計は70.06:29.94です。
比べてみると勝率はa<bでおおよそ5%ほど勝率の差が生まれました。条件のひとつである比重がそれぞれほぼ同一で見ているのでこうなっていますが1000持ちに対してaなら確定リーサル、bでも敗率6%と考えると1000持ちには両パターンでもほぼ勝てることが分かります。それならば、比重から1000持ちのパターンを抜いて2000or3000持ちに対してどれくらいの差があるのかを比べることでより判断の材料に組み込みやすいと考えられるので比重を2000,3000持ちにそれぞれ半分ずつ振り分けて計算した場合こうなりました。

11%も勝敗に差が生まれました。この状況のポイントとしてaは2000持ちにほぼ勝つが、3000持ちに必敗。これに対してbは2000には7割強かつ上に3000持ちに対しても4割は勝てるというところだと思います。
ちなみに比重ではなく確率で求めても8000,8000のほうが勝率は高いです。
7000,9000という階段の段差の理由を考えるとライフが2000であっても貫通するからとよく言われたりしますが実は誤りです。そもそも7000が通るということは相手は3000も持っていない状況なのでライフがどうであれ7000が通ったならほぼ勝ちです。つまりは相手が3000持っていないことを決め打って動いているためライフの数値はほぼ関係ないのです。
対して8000,8000はライフが非カウンター値なら3000持たれていても勝つものの2000持ちに対してはライフが2000だった場合に負ける。わけですから単純に考えると非カウンター値と2000カウンターどっちが多いのかで段差を付けるかどうかの判断ができるということです。
逆に言えばライフが2000じゃないなら階段に2000の打点差をつける必要はありません。
この観点からデッキの構成から非カウンター>2000カウンターという枚数なら8000,8000、枚数関係が逆なら7000,9000と言われたりしますが実はそうでもないのではないかと思います。

こちらを見ていただきましょう。条件は現環境デッキでもあり非カウンター<2000カウンターの枚数関係というかなり珍しい構築になっている赤紫ローと想定しています。1000カウンターが20枚、2000カウンターが16枚、非カウンター値が14枚とします。
簡易的に示した表になりますが上が7000,9000のパターンで下が8000,8000のパターンです。
手札は2枚という条件で手札1枚目、2枚目とライフ1の数値分布によって各パターンで左に敗率が表示され太枠にそれらの合計が記載されているという読み方です。まあ表は見れなくても問題はありません。
非カウンター値と2000カウンターの枚数関係が<であるにも関わらず8000,8000の振り分けのほうが若干勝率が高く算出されています。また、条件である手札2枚というのはこれ以上枚数を増やしたところで初動のアタックが止まるパターン(1000×3枚等)が増えるだけなのでこの勝敗率の上下関係が覆ることはありません。
と、いうのも7000が止まるハードルと8000が止まるハードルは比べるまでもなく前者のほうが低くそもそも最初に止まりやすいのは前者です。このハードル差+非カウンター値と2000カウンターの枚数差を両立させて考えるとこの程度の枚数差なら8000,8000のほうが優位であることは変わらないようでした。
つまり階段に2000差つける必要があるパターンは現状限りなくないと言って問題ないでしょう。今後2000カウンターが20枚になって非カウンター値がほとんど入らないといったインフレ環境になってから再度考え直すとします。
固定観念で段差を付けるほうがいいと考えるのではなく、なぜその打点差をつけるのかを考えると実戦においても判断を誤りにくくなります。理由を自分で理解することでその状況に応じて公開されている情報からの判断にも寄与してくれることでしょう。
6.段差の位置
かなり前ではありますがこんなシーンのツイートがありました。

盤面的には相手にブロッカーが2体いる+ライフが2枚の状態であるため手札からホーディを出してリーサルへ向かうところまでは確定しているもののリーダーヤマトで振るドンをどこにつけるのか、や9ゾロのアクティブ効果を何回使用するのかといったところの判断が複雑な状況です。
ホーディを出すのか確定と言いましたが一応整理します。
現状の相手の無限カウンターは4回分であり、こちらのアタック回数はホーディを出さないのであれば最大5回となります。振り分けはとりあえず適当に9000,9000,10000,10000,10000くらいにしておきます。
このうち後ろ4回分のアタックが無限カウンターによって止まるため、要求値は9000に対する5000であると推定できます。細かい階段が必要かどうかとかは後でホーディを出さない選択肢になったときに計算します。
では続いてホーディを出すパターンです。
ここまでの解説からまず初めにやることはライフを用いた無限カウンターはどのアタックを吸うのか、相手は何回手札で攻撃を止める必要があるのかの整理です。
今回の場合はまず余った3ドン及びリーダー効果で付与できる2ドンは一旦置いといて整理しましょう。
5000,5000,8000,9000のアタックに対して相手のライフが2枚あるため、相手が手札で攻撃を止めなければいけない回数は2回となります。ライフに対して8000,9000が突っ込む形になるので現状の要求値は1000+1000の合計2000であることが分かります。
これに例えば残っている5ドンを付与した場合、均等に5000に振り分けると相手が手札で止めなければいけないアタックは7000,8000となり、要求値は7000になります。これは付与した5ドンが要求値になったということです。
つまり現状は5000,5000+5ドンが要求値になっていると理解できます。ホーディは既に出したほうが強いことがわかったため出さない選択肢は捨てます。
では続いてはゾロを1回起こすパターンを考えてみます。
5000,5000,8000,9000,9000のアタックになり、ライフで止まるはずだった8000,9000は9000,9000が止まることになります。9000に押し出されて要求値に8000のアタックも加わることになり、要求値は5000,5000,8000+4ドンが要求値となりました。
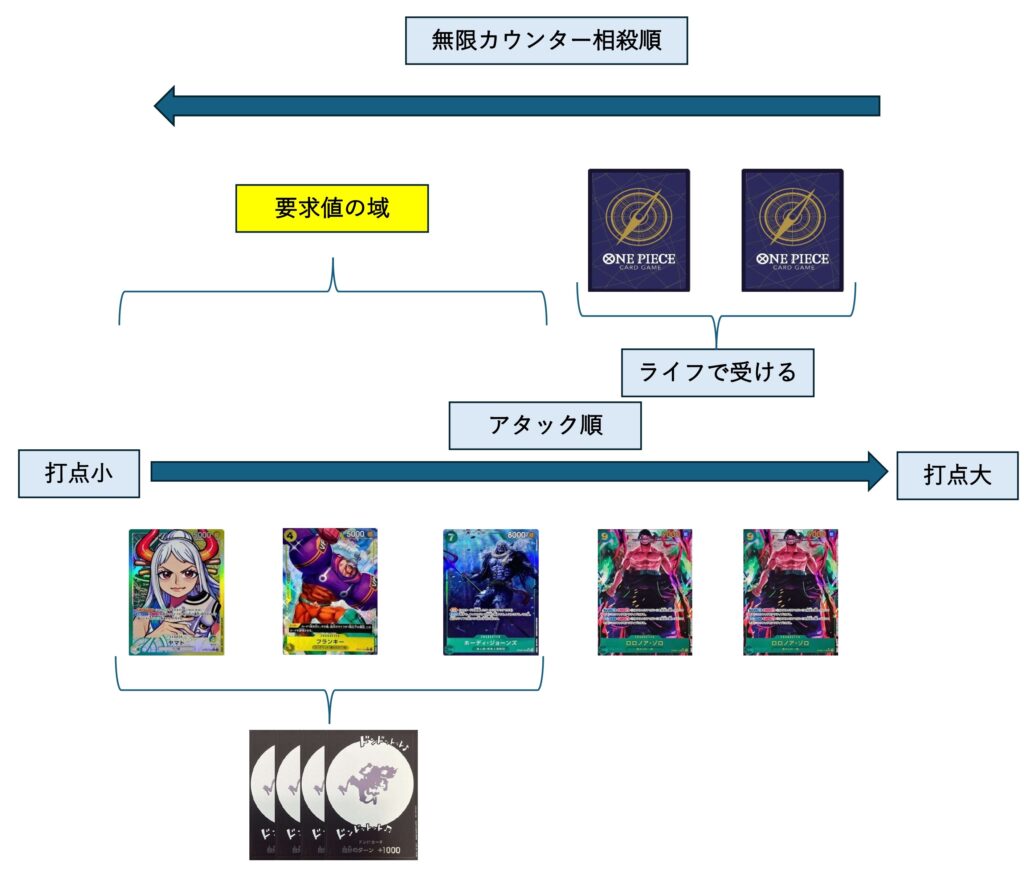
3項の解説通り背の順に並べて止まる位置を整理します。アタック回数が増えれば前に並んでいるアタッカーは押し出されて要求値に入ってきます。
1ドン使用して起こすことで、5000,5000+5ドンの要求値を5000,5000,8000+4ドンの要求まで上げることが出来たため、ゾロは1回起こしたほうが得であることが分かります。
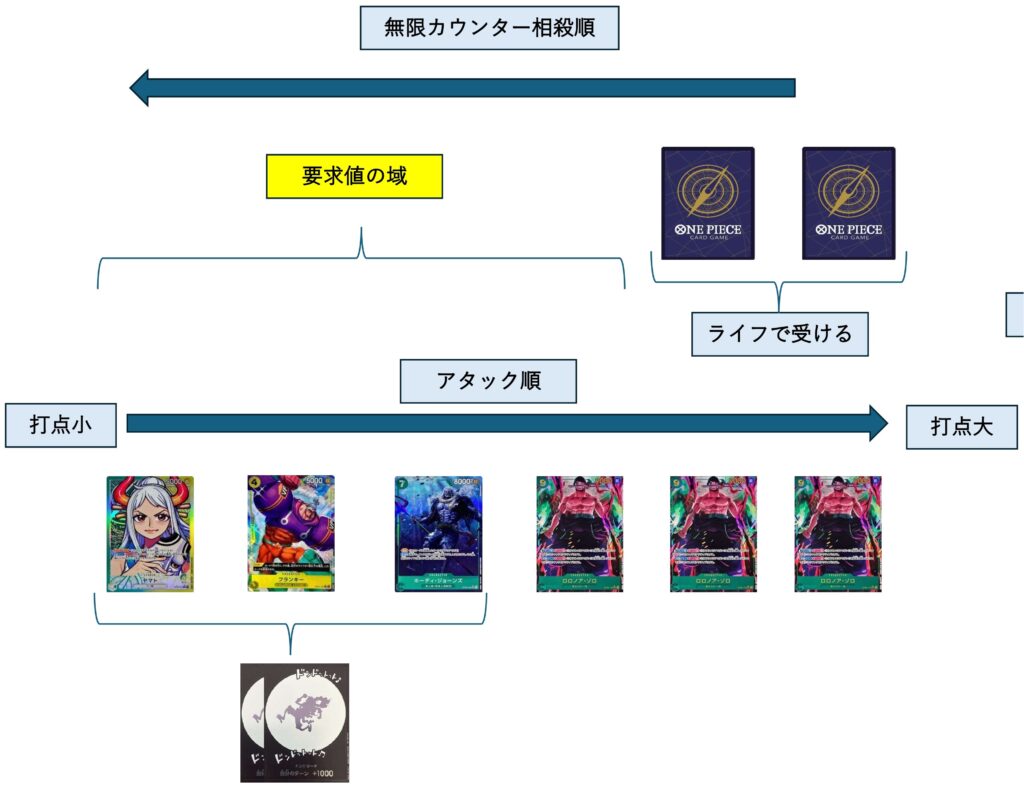
続いて、ゾロ2回起こすパターンですね。またもや押し出されて5000,5000,8000,9000+2ドンが要求値になることが分かりました。2ドン使用することで9000を要求値に含めることが出来るためゾロは2回起こすのが最大になるようです。
この整理の方法を見ると、攻撃回数が多くドンを振るとお得そうなゾロにリーダー効果でドンを振っても結果的に相手の要求値に加わるアタックは1回分でしかないため要求値上はゾロに振っても得をするわけではないということが明確に分かります。損をするわけでもないのですが。
続いてはどこにドンを付与するかの整理を行います。
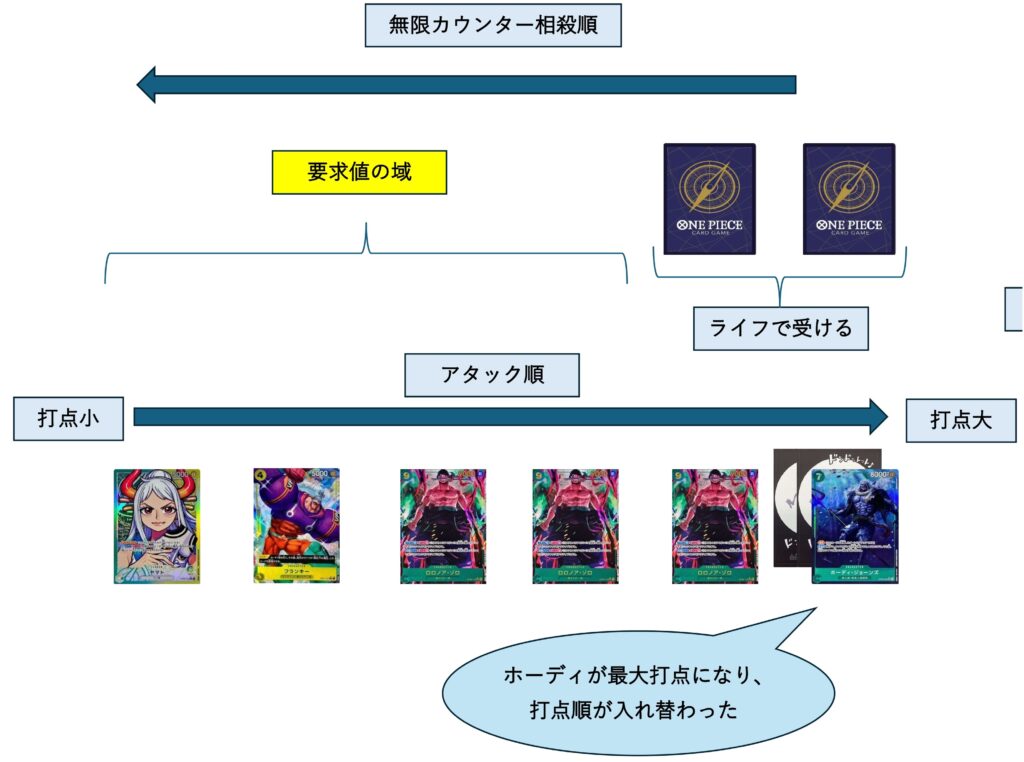
ドンを付与できる3択のうち唯一損をするところがあるので先に挙げますが、ホーディにドンを振ると打点の並びが5000,5000,9000,9000,9000,10000になります。2ドンを振ったことで要求値になる枠が8000と9000が入れ替わるだけになるので1ドン分損であることが分かりました。
ではフランキーとゾロどちらにドンを付与するかです。
今のところ5000,5000,8000は手で止めて9000,9000をライフで受けた後に9000を手で止める状況だと整理することができますがフランキーに2ドン振ってもゾロに2ドン振っても要求値はそれぞれ5000,7000,8000,9000or5000,5000,8000,11000であるため全く変わりません。
つまり今回のケースではホーディを出してゾロは2回起こしてフランキーかゾロのどちらかにドンを振れば要求値最大が取れるというわけです。
しかし、フランキーゾロどちらにドンを振るかは要求値には現れませんが明確にフランキーに振ったほうがいい理由があります。
これはシンプルにライフ無要求値が高いからです。
ライフを加えない状態で止めなければならない打点が高ければ当然その分8000のアタックが通りやすいので要求値は上がりやすいんですね。
極端な話、相手のライフが両方とも3000カウンターであったと仮定した場合を考えると、ゾロに振る場合は相手の手札が1000×3+2000×2でも止まってしまいますが、フランキーに振る場合は1000×3+2000×2では8000が止まらずに9000,9000に対して1000足りずに貫通となります。
相手のライフが両方とも2000であったと仮定した場合、相手は手札に1000×3、2000×3の合計9000が止まるラインになりますがこの場合は2ドンをどちらに振っても守られます。ライフの数値が大きければ大きいほど段差が手前にあることが効いてくるという性質により、逆にほとんどの場合に差は生まれません。
と、ここまで理解したうえでちょっとミソな部分がありまして、これリーダーアタックしたあとにフランキーに2ドン振って7000から入るのでなく、ホーディの8000からスタートするのが一番高くなるのです。
フランキーに振ってもゾロに振っても手から守られるのは同じ2ドン分としましたがもしホーディの8000が通ってライフを取れた場合、ゾロの3回アタックのうち2回は手で止めなければいけなくなるわけです。そうなるならフランキーに振るよりもゾロに振った方が2ドン<2ドン×2で要求値高くなります。
ホーディのアタックが守られた場合はフランキーに振って7000でアタックすれば当初の予定通りなので何の問題もありません。
これは4.1項の応用です。
今は素の数値と0イベしか考慮していないため大きく影響はないように見えますがドンが起きていて、イベントカウンターがあるかもしれない状況だとこのくらいの差でも落とすゲームが存在します。細かいミスで落とすのはもったいないので要求値が同じなら段差は極力手前に持ってくる。これは忘れずに意識しましょう。
7.小さな打点で上がる要求値
こちらは以前僕自身も記事にした内容となります。
時間がある方は一度目を通していただくとさらに分かりやすいとは思いますがこれを見ずとも本記事にて再度0から解説していこうと思っております。よろしくお願いします。
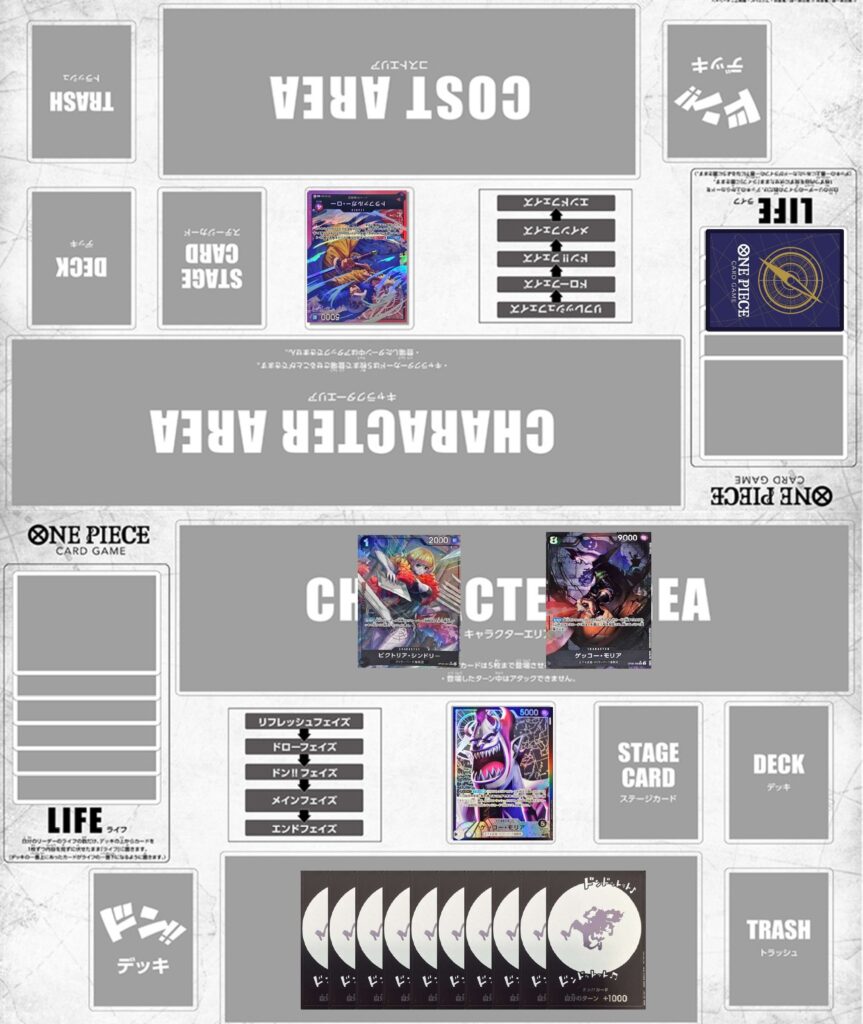
例としてこちらのシーンを用います。盤面は2000,9000のキャラと5000リーダー+10ドンで、相手のライフは1枚という状況です。基本的なアタッカーの数を考えると相手が手札を使用して止めなければならないアタック回数は1回となります。
ここまでの解説通りに行けばリーダーとモリアにドンを割り振って12000,12000の8000要求でしょうか。いや、シンドリーにもドンを振って8000,9000,9000で4000+5000の計ライフ1込9000要求のほうが強いですね。
実はこれ10000要求まで上げることが可能となっています。
10000,14000or10000,8000,8000の振り分けが理論値の10000要求となっています。
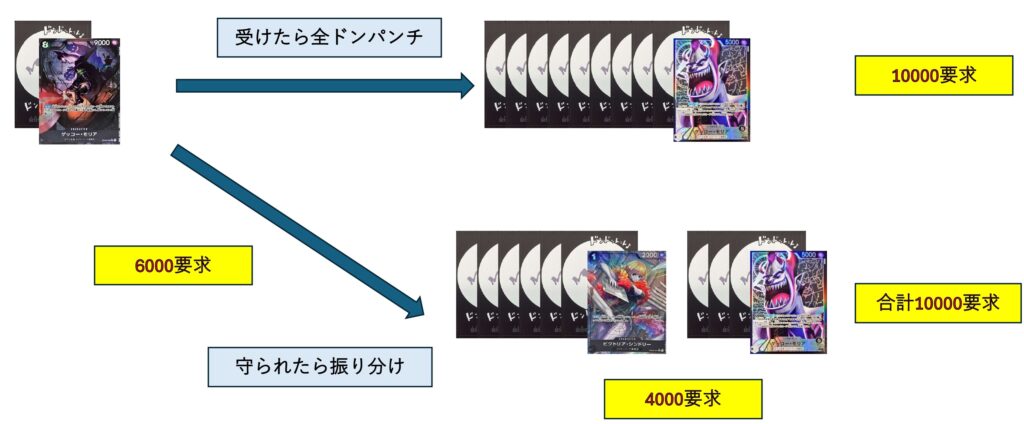
モリアに1ドン振って10000でアタックし、通れば残り9ドンをリーダー付与して14000アタックのライフ1込10000要求となります。もし10000アタックが6000切られて止められた場合はリーダーとシンドリーにそれぞれ均等にパワーを振って8000,8000でアタックすることで4000要求となり合計でライフ1込10000要求となりました。
これ場のシンドリーが仮に0打点であったとしても要求値を上げることが可能です
もし0のキャラだった場合は3体に普通に振っても7000,8000,9000のライフ無7000~ライフ1込8000要求、もしくは普通にアタッカー2体に振ったこれもライフ1込8000要求です。
が、これも10000,14000or10000,7000,7000でライフ1込9000要求まで上がります。
先ほど同様に10000アタックからスタートし、止まった場合は7000,7000で割り振ることで6000+3000の計ライフ1込9000要求となるわけです。
本来アタッカーになり得ない2000のキャラや、あまつさえ0のキャラさえもがアタックに参加することで要求値が上がるため直感に反していることからこれを知らないという方がかなり多くいるようなのでここで完璧にマスターしていきましょう。
さて、本項1つ目の例に戻り、まずはなぜこんなことが起きるのかを解説していきます。
本記事では序盤に打点の振り分けは大きくないほうが良い、と記載しました。極端な話、5000,19000のような振り分けは要求値が1000~15000となるものの当然1000で止まってしまうからです。逆に5000が通れば要求値は一気に跳ね上がります。
徐々に平均打点に近づくにつれて打点の振り幅も小さくなり、守られても通っても要求値の振り幅も同様に小さくなっていきます。
ここで大事なのは1回目のアタックに関していえば平均打点より小さい打点のアタックが通ればこちらは得をする、ということです。逆に平均打点より大きい打点のアタックを守ってもらっても同様に得をします。
この性質を利用することが要求値を上げる方法に繋がります。
リーダーとモリアのアタックの平均打点は(5000+9000+10000)/2=12000となります。また、リーダーモリアシンドリーの3体アタックの平均打点は(2000+5000+9000+10000)/3=8667となりました。
2体アタックの平均打点と3体アタックの平均打点の間に位置する9000~11000の打点でアタックすることで通れば2体アタックの平均打点より低く通ったため得、守られた場合に3体アタックの平均打点よりも高い打点を守らせたので得、というふうにどちらに転んでも要求値得するようにすることが可能です。
これこそが小さな打点で上がる要求値になります。
ではこの打点の求め方を解説します。
先ほどは両パターンの平均打点の間の9000~11000と記載しましたが実際に理論値を求めるためには計算が必要になります。
a=(x-y+8000)/b
a=1回目アタック打点,b=総アタック回数,x=基本アタッカー含めた合計打点,y=小さいキャラの打点
上記の式から求めることが可能です。
本項例を当てはめてみると、bは小さいキャラ含めたアタック回数の3、xは5000+9000+10000=24000、yはシンドリーの打点となるので2000です。計算をしてみると(24000-2000+8000)/3=10000となり、a=10000と算出することが出来ました。

他の例を用いて計算してみましょう。状況は同様に相手のライフは1枚、こちらのアタッカーは5000のリーダーに加えて6000,9000,2000のキャラの4体となっています。
通常の振り分けであれば9000,10000,11000でライフ無11000~ライフ1込12000要求といったところです。
先ほどの計算式を用いて計算してみます。x=5000+6000+9000+10000=30000、y=2000、b=4となります。
上記を式に代入するとa=(30000-2000+8000)/4=9000となりました。もしaが1000単位で割り切れない場合は四捨五入します。いやワンピースカードでいうなれば499捨500入ですね。
9000が通れば6000,15000の合計13000要求となります。もし守られた場合はxから9000を引いたあとの状況を再度計算式を用いて算定します。
先ほどのアタックでxから9000分なくなった、またアタック回数も1回分減ったのでbが1減り、a=(30000-9000-2000+8000)/3=9000となりました。2回目のアタックも9000でいきます。
この9000が通った場合残りの全ドンパンチは12000となるため、先ほどの9000へのカウンターも含め5000+8000の計13000要求となります。
また、この9000も守られた場合はリーダーとシンドリーにそれぞれ打点を均等に振り、7000,7000となるので要求値は5000+5000+3000で計13000要求となりました。
やはり通常の振り分けよりも高い要求値が出ました。
また、こういった要求の計算の際に相手がどこで守ったかによって要求が若干変動する場合がありますが相手の守った箇所によって要求値に2000以上の差が出る場合は計算に間違いがある可能性が非常に高いです。
理論値であれば要求値の振り幅は1000以下に収まるはずなのでこれを頭に入れておくと実際に計算した際に間違っていないかどうかの確かめが可能です。
実戦でこんな計算までしろとはいいませんがこの守った箇所による要求値の振り幅という点については覚えておいていただきたいです。ここで止まったらいくつ、ここで止まったらいくつというパターンを計算して止めた箇所によって要求値が大きく異なるのであればそれは理論値にはなりません。差が1000以内に収まっていることを確認しましょう。
本項1例の5000,9000,2000という盤面であれば計算式を使用せずとも手動の割り振りでも求めることは可能です。2体アタックの平均打点より低くという性質を利用しているため、2体に通常の振り分け、本項1例の場合は12000,12000という打点を作ってから1ドンずつずらしながら計算することで求まります。
11000からだと、通れば13000の9000要求。止まったらそのあと7000,8000で7000+3000or4000の10000~11000要求。9000要求と10000~11000要求は差が2000あるので×。
再度1ドンずらして10000から、14000の10000要求、止まったら8000,8000で6000+4000の10000要求で差が0なので理論値。
といった具合です。
そうしたときに各パターンの要求値を求めて振り幅を確認すれば計算式なんて覚えなくても理論値で要求値を導けます。
なぜこういったことが起きるのか、ということと要求値の振り幅さえ覚えておけば実戦時にでも使えるようになるはずです。計算式はいつか楽するために覚えるくらいで。
小さいキャラがいてアタック回数に余剰があるときは意識してみてください。
7.1小さいキャラが複数体の場合
もうこれ以上計算式は覚えなくていいですし結局レアケースだとは思うので読み飛ばしても大丈夫です。
ただ、一応要求値は上がるので覚えるに越したことはありません。

同様に相手ライフは1、こちらは5000,9000,3000,2000となっています。
こういった小型が複数体いる場合の計算式はこうなります。
a=(x-2y-z+20000)/b
各係数は先ほど同様です、z=追加の小さいキャラの打点
これを用いて計算すると、x=5000+9000+10000=24000、y=3000、z=2000、b=4となります。
代入すると、a=(24000-2×3000-2000+20000)/4=9000となりました。
1回目のアタックは9000で通れば全ドンパンチ15000の11000要求で、守られた場合は再度計算です。
先ほど同様xから9000を除きますがxに3000追加しなければなりません。2000があくまでアタックするかどうか変わってきますが3000のキャラは既にアタックが必須となっているためアタッカー打点としてxに加える必要があります。状況は9項と同様になったため、計算式はa=(x-y+8000)/bを用いることになります。このxからaを引いて3000足すことが必要なわけです。
a‘=(24000-9000+3000-2000+8000)/3=8000となりました。
通れば全ドンパンチ10000の計5000+6000で11000要求で、守られた場合はブランニューとシンドリーに均等に割り振り6000,6000のアタックとなります。5000+4000+2000で計11000要求となりました。
9000,15000or9000,8000,11000or9000,8000,6000,6000の11000要求ですね。9項同様に10000からスタートすると10000要求になる箇所が生まれるのでやはり小さいキャラが2体目いるだけでも要求値は1000上げることができるようです。
小さいキャラが複数体いる場合は9項の式では成立しないため別途で専用式を覚える必要があります。ここまでくるともう覚えとかなくても…とは思います。が、つい最近これのおかげでフラッグシップでギリ勝ったのでやっぱり覚えるに越したことは…。
特に黄黒ルフィ対面には頻発していて、相手リーダーの打点が4000上がる。これは言い返せば5000リーダーに対してこちらの盤面のパワーが全て4000下がっていると解釈して考えることが可能で、このような状況では小さいキャラがアタッカーとなる場面がかなり多いです。
7.2相手のライフが2枚ある状況
ここまでは相手のライフが1、つまり無限カウンターが1回分あった状態を例にしてきましたが今回は2枚の状況で解説していきます。
本項も計算式を使います。許してください。

こちらの盤面5000,6000,9000,2000という状況です。
普通に振り分けるとライフがあるので階段で9000,10000,11000のライフ無5000~ライフ2込7000要求でしょうか。小型もアタッカーにした7000,8000,8000,9000のライフ1込7000~ライフ2込8000要求のほうが高そうですね。
これは8000,9000,13000or8000,9000,7000,8000or8000,7000,8000,9000でライフ無7000~ライフ1込8000~ライフ2込9000要求になります。
a=(x+4000)/4-1000
計算式はこうです。小さいキャラがいるにもかかわらずy係数を使用しないで計算することになりました。なんでなのかは僕も不明です。
-1000に関してはライフ分の要求値につける階段を表しています。ライフが2枚ある場合、どこで守られても要求値のパターンは1000差以内に収まるという点を満たしてしまうとライフ無とライフ2込の要求値が1000しかない場合相手としてはライフ2込の要求のほうが安くなってしまい、理論値から離れてしまうためです。
守られた場合は余剰のアタック回数がないのでシンプルに階段振り分けになりますね。
1回目のアタックが通った場合はライフ1に対してアタックが3回残っている9項の条件になるため同様にa=(x-y+8000)/bを用います。
xからaを引くのを忘れずに計算しましょう。攻撃終わるたび都度xを計算しなおせば間違えることはないと思います。
では改めて振り分けの計算をしてみようと思います。a=(x+4000)/4-1000で1回目の数値を出します。xは5000+6000+9000+10000の30000と出ました。(30000+4000)/4-1000=7500≒8000なので1回目のアタックは8000です。
通れば9項の条件と同じであるためa=(x-y+8000)/bを用いて、(30000-8000-2000+8000)/3=9333≒9000で2回目のアタックは9000と出ました。
これが通ればあとは全ドンなので13000のライフ2込9000要求です。
もしこの2回目のアタックが止まっていた場合は相手のライフ1枚に対して残っているアタック回数は2回で余剰はないのでシンプル振り分けの7000,8000で9000に対する5000+3000~4000でライフ1込8000~ライフ2込9000要求です。
1回目のアタックが止まっていた場合はライフ2枚に対して残っているアタック回数は3回で余剰はないのでシンプル振り分けの7000,8000,9000で8000に対する4000+3000~5000でライフ無7000~ライフ1込8000~ライフ2込9000要求です。
注意していただきたいのは今回の場合どの振り分けパターンにも9000打点でのアタックがあったためモリアはちょうどよくアタック出来ていましたが、これがもし8000,6000,7000,7000のような振り分けが算出された場合に9000という打点はどこかで過大になってしまい、逆にその差の分どこかの打点が下がってしまいます。そういう場合は一番最初のアタックに使用してしまうのが良いと思われます。これは本項の例だけではなくどの例にも言えます。
まあ、4~5回アタックでもしない限り過大になることはたぶんないです。
7.3計算について
本項では計算式についてなぜこれらの係数で求まるのか、+8000や+4000というどこから来たのか分からない項についての解説をしていこうと思います。
これが分かれば自身の検証でも用いることができ、他パターンではどう求めればいいのかわかると思います。とんでもなく勉強熱心なら読む価値ありますが、これらは読まなくても100%問題ありません。
まず9項の計算式、a=(x-y+8000)/bについて解説します。状況も同様に9項を用います。
10000,14000or10000,8000,8000という打点はそれぞれα,β or α,β‘,γ’とします。
要求値はどのパターンをとっても等しくなるという性質を利用すると、β-4000=α-4000+β‘-4000という等式で表すことが出来ます。
14000-4000=10000-4000+8000-4000と当てはめれば10000=10000となりますね。分かりやすくいうと大パンチ=中パンチ+小パンチです。
ここからαについての式にすることで盤面の状況から最初のアタックの打点を導きます。
βはαが通ったあとの全ドンパンチであることから合計打点からαを引けば算出が出来ます。リーダー5000とモリア9000+10ドンの合計打点は24000なのでモリア10000アタックが通ればリーダー14000の全ドンパンチであるというのは誰しもが理解できると思います。
なのでβ=x-αの式で表すことが出来ました。
β‘はαが守られてしまったあとの残りの打点でγと振り分けて打点を作ります。モリア10000アタックが止まってしまった後はリーダーとシンドリーに均等に振り分けて2回アタックする状況なのでこれもわかると思います。
つまりβ‘は合計打点からαが引かれたあと、yを足して2分割すれば求めることが出来ます。
なのでβ‘=(x-α+y)/2の式で表すことが出来ました。
β-4000=α-4000+β‘-4000
先ほどのこの式に以下を代入することでαについての式とすることが可能です。
- β=x-α
- β‘=(x-α+y)/2
x-α-4000=α-4000+(x-α+y)/2-4000
次に分数を消すため両辺に2を掛けます。
2x-2α-8000=2α-8000+x-α+y-8000
各係数をまとめると同時にαについての式にします。
-2α-2α+α=-2x +8000-8000+x +y-8000
あとは整理します。
-3α=-x+y-8000
両辺を-3で割ります。
α=(x-y+8000)/3
となりました。分母が3なのは総アタック回数が3回だからで、9.1項のように4体アタッカーがいる場合は4になります。アタック回数が増えればその分そのアタックを示す式にαが登場するためこの1式前の段階の左項が-4αになるわけですね。
9.1項のα=(x-2y-z+20000)/βも同様のやり方で求めることが出来ます。
おそらく小さいキャラが増えればその分-3y-2z-vと項が増えていき、それに伴い変数もそれぞれ1ずつ上がっていくと思われます。また、+20000の部分は4000nでnは等差数列だと思います。b=3ではn=2でしたが、b=4ではn=5でした。検証していませんがb=5のときはn=9となると思います。2,5,9,14,20となっていくと思いますがここまで増えるとドンが足りないので考える必要はありません。
9.2項のa=(x+4000)/4-1000についてです。
アタッカーが4体なのでα,β,γorα,β,γ’,δorα,β‘,γ’‘,δ‘とします。
8000,9000,13000or8000,9000,7000,8000or8000,7000,8000,9000でしたね。
γ-4000=α-4000+γ‘’-4000という式にします。
後は同じです。
γ=x-α-β、β=(x-α+8000-y)/3、γ’‘=(x-α+y)/3
それぞれこう表すことが出来るので代入していきます。
x-α-(x-α+8000-y)/3-4000=α-4000+(x-α+y)/3-4000
こうなって
3x-3α-x+α-8000+y-12000=3α-12000+x-α+y-12000
こうなって
-3α-3α+α+α=-3x +x+8000-y+12000-12000+x+y-12000
こうなって
-4α=-x-4000
こうなって
α=(x+4000)/4
となりました。
これにライフ2あることから数値上は等しいもののライフ無とライフ2込の要求値をそのライフ分に合わせるためにαの打点を1000下げて調整した結果α=(x+4000)/4-1000となるわけです。
こういった数式を用いることで理論値を計算で導き出すことが可能です。ゲーム中にこれらをするわけではなく、事前にこのパターンのときはどの数式で理論値が出るかという準備のためです。
念のため僕自身は9項~9.2項までの3パターンは最低限暗記しています。
暗記せずとも9項の理論をとりあえず理解できればその場で計算も可能ではあるので理論だけでも覚えておきたいところです。
8.無限カウンターへの除去
これまでリーサルターンのアクションはアタックの打点のみしか考えていませんでしたが近年では相手のブロッカーをレストにするだとか、KOするだとかでアタック前に必要なアクションが増えてきました。
アタック回数的には足りてるのでKOしなくてもいいが、どっちのほうが要求値が高いのか悩むことがあると思います。
相手の無限カウンターの枚数に対してこちらのアタック回数が余剰が生まれていないなら脳死で除去は必要です。
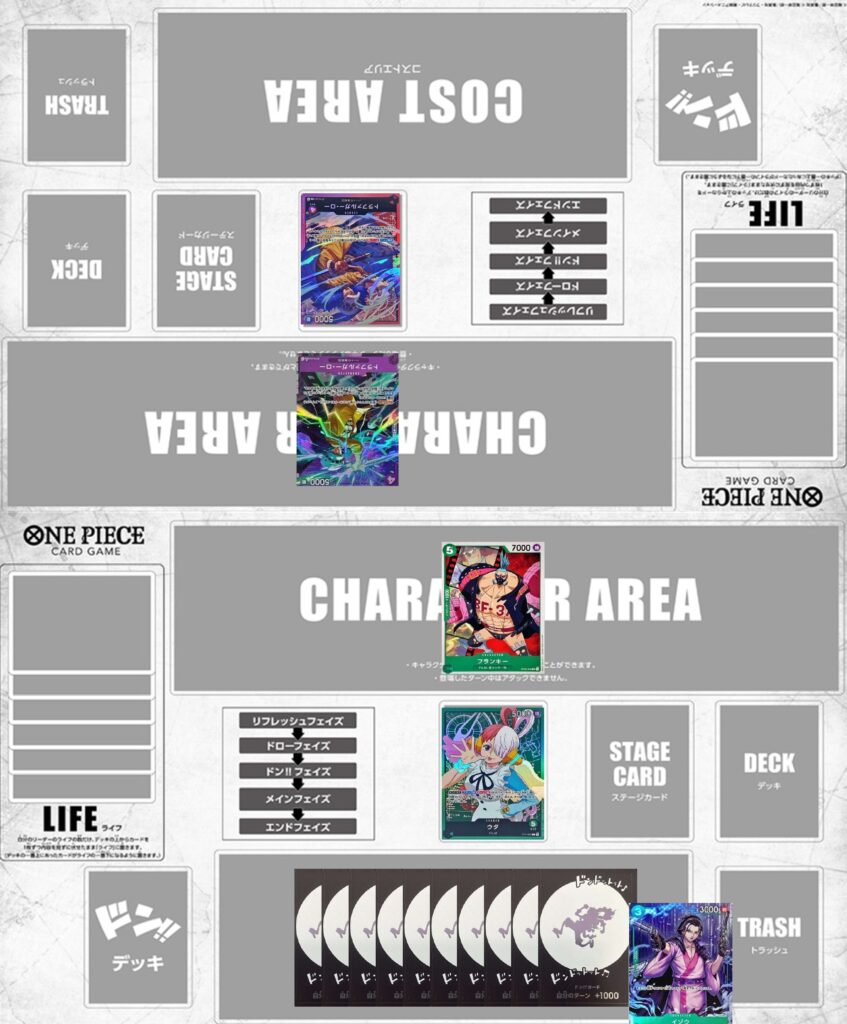
ではまずシンプルに打点は足りてるものの、イゾウで相手の無限カウンターを1回分消すことで要求値はどうなるか考えてみます。
まず、相手のライフは0でブロッカーは1体。対してこちらはアタッカーは5000,7000と手札では3ドンで相手のブロッカーを無力化することが出来る状態です。
シンプルに振り分けるなら11000,11000で1回分はブロックなので要求値は7000です。
これが3ドンでレストにしてからアタックした場合は5000,14000がどちらも要求値になるため、1000+10000の合計11000要求となります。
この時点で無限カウンターは無力化できるなら無力化するのが良いとわかります。当然11000という7000要求一回分の無限カウンターを3ドンで阻止できるのであればその差の4ドン、つまり4000分が要求値に乗っかってくるからですね。
で、たまーに悩むのがレストにさせずにアタックしてブロックしてきたら全ドンパンチ、ブロックしてこなかったらレストにして全ドンパンチって択だと思います。
これ実は先にレストにしても後にレストにしても要求値はお互いに理論値を取った場合11000から変動しません。
どういうことかというと1回目のアタックの打点がなんであれ手札で止めれば相手は絶対にレスト札を使用せざるを得ないため、結果としてついてくるのは5000,7000+7ドンが要求値になることから変わらないからです。
ただ、これには条件があり、最初のアタックの打点を極端に大きくしてしまうとブロックされた場合に要求値が下がってしまいます。
最初に9000でアタックしてブロックされた場合、イゾウは出さなくてよくなったものの、この後の全ドンパンチの打点は14000で要求値は10000にしかなりません。
お互いに理論値を取った場合というのはこちらの1回目のアタック打点がブロックされない打点で相手は損をしないように手札で守る限り、ということになります。
ちなみに最初のアタック打点の条件についてですが、これは無限カウンターを無力化するために使用するドン+4000打点以下であることです。
今回の例でいけばイゾウを使用するための3ドン+4000なので最初のアタックの打点は7000以下でなければいけないわけです。
これを利用して、どうせ要求値が変わらないなら先にイゾウを出すよりも5000~6000でアタックしてもし相手がブロックしてくれたらイゾウ出さない分要求値上がったラッキー程度にアタックするのが良いでしょう。
上記は無限カウンターが他にない状態の話なのでまだライフが残っているとかであれば適当に5000でアタックしよ~はだめですよ。
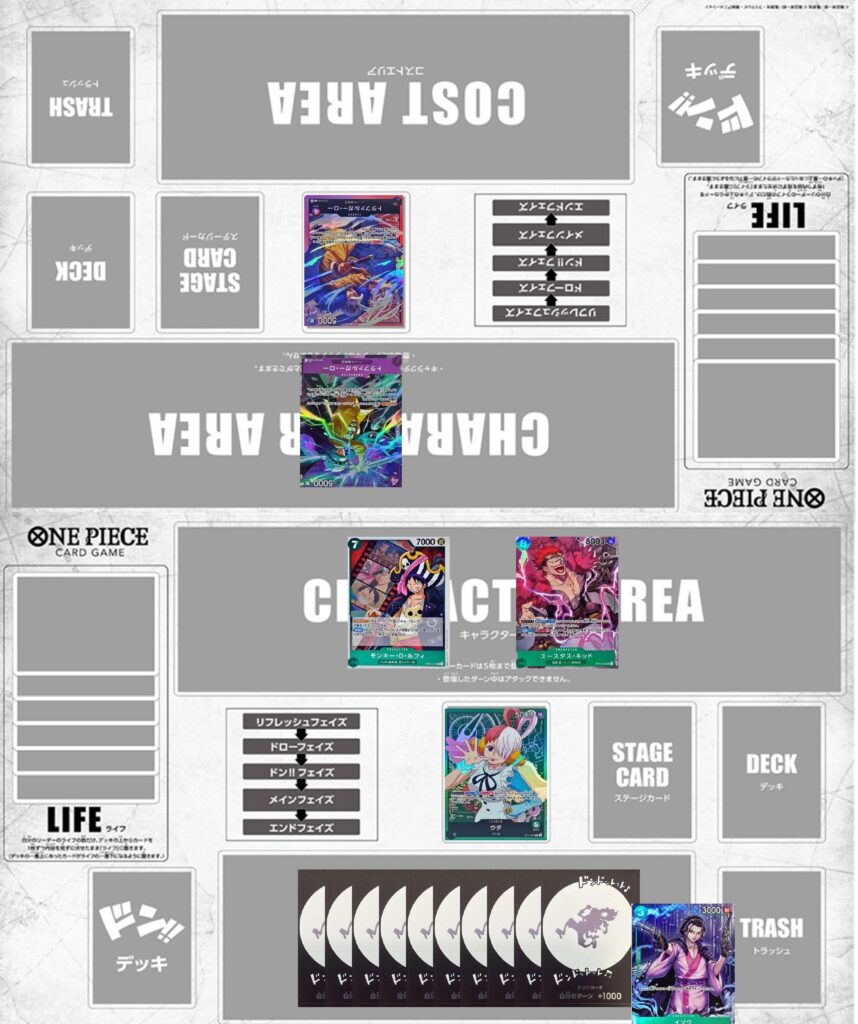
こういった場合はどうでしょう。相手のライフは1枚、ブロッカーは1体に対してこちらのアタッカーは5000,7000,8000で手札には同じくイゾウです。
明らかにイゾウを使用してブロッカーをレストにするのがよさそうには見えますが一応計算してみます。
レストにせずにそのまま突っ込む場合これは3.1項の教えの通り均等でいくのが一番高いので10000×3でアタックとなります。このうち1回分が要求値になるため6000となります。
レストにしてアタックすると、相手のブロッカーが0になるためアタック3回のうち2回が要求値になります。3ドン分打点は下がりますが9000×3で5000×2の10000要求となりました。歴然の差です。
この場合に関してはアタックしてからブロックしなければレスト、みたいな択はありません。絶対に先に無限カウンターを無力化してからアタックです。
打点を少し小さく先にアタックしてそれが手札で止められた場合にレスト札を使用することになりますが、そのせいで相手が1回分手札で止める打点を小さくできているせいで平均打点に対して無限カウンターが吸うことになる数値が大きくなってしまうためです。
相手の無限カウンターが0枚にならないなら先に無力化できる札は先に使用するのが良いでしょう。 たまーに除去を使う使わないの瀬戸際打点を作ることで要求値上がるときがあるみたいなのを見たことある気がしますが、僕はまだ出会ったことがありません。誰か知ってたら教えてください。
9.まとめ
ここまでがおおよそリーサルに関するあれこれです。あとは実際の場面でどこから考えたらいいのか、どういう流れで打点を決めているのかを解説していきます。
6項では僕が普段思考している流れで考えてみましたが改めて。
おおまかな流れとしてはこうなります。
現状の無限カウンターの枚数とこちらのアタック回数から相手が止めなければいけないアタック回数を確認
↓
シンプルに均等に打点を割り振って要求値を算出
↓
状況に合わせて階段or均等、除去は打つor打たない、小さい打点のキャラがリーサルに関与するかなどの情報を付け加えて最終的な打点を算出
基本的には上記の2つの工程が必須でこの後に、除去を打ったり、9ゾロを起こした時を考えたり、速攻を出したり、小さい打点をアタッカーにする必要があるか考えたり、とその場の状況に合わせて付随されていくという認識ですね。
2工程目のとりあえず均等に打点を割るというのが特に大事で、ここで出た打点をベースに考えるのを始めるのが時間効率的にも一番いいかなと個人的には思っています。
また、最終的に決めた打点が他のパターンに比べて劣っていることがないかは絶対に確認してください。
誤ったリーサルをしてしまう人は特に確かめを行えていない場合が多いです。リーサルターンはどんなに時間をかけてでもいいので理論値出るまで熟考です。そのためにもそれ以外では時間を使わないように心がけています。
10.あとがき
とてつもなく長かったとは思いますがここまで拝読いただいた方には感謝しかありません。僕が出せるリーサルのあれこれは限りなく出し尽くしたかなと思います。読みにくい部分ばかりかもしれませんが時間かけてでもリーサルのミスが一つでも減ればうれしく思います。
もし不明な点や、こういうときどうしたらいいかなどの疑問については気軽にお声掛けいただければ回答したいと思います。
ありがとうございました。そりでは~
おすすめ記事(基礎を学んだあなたに!)